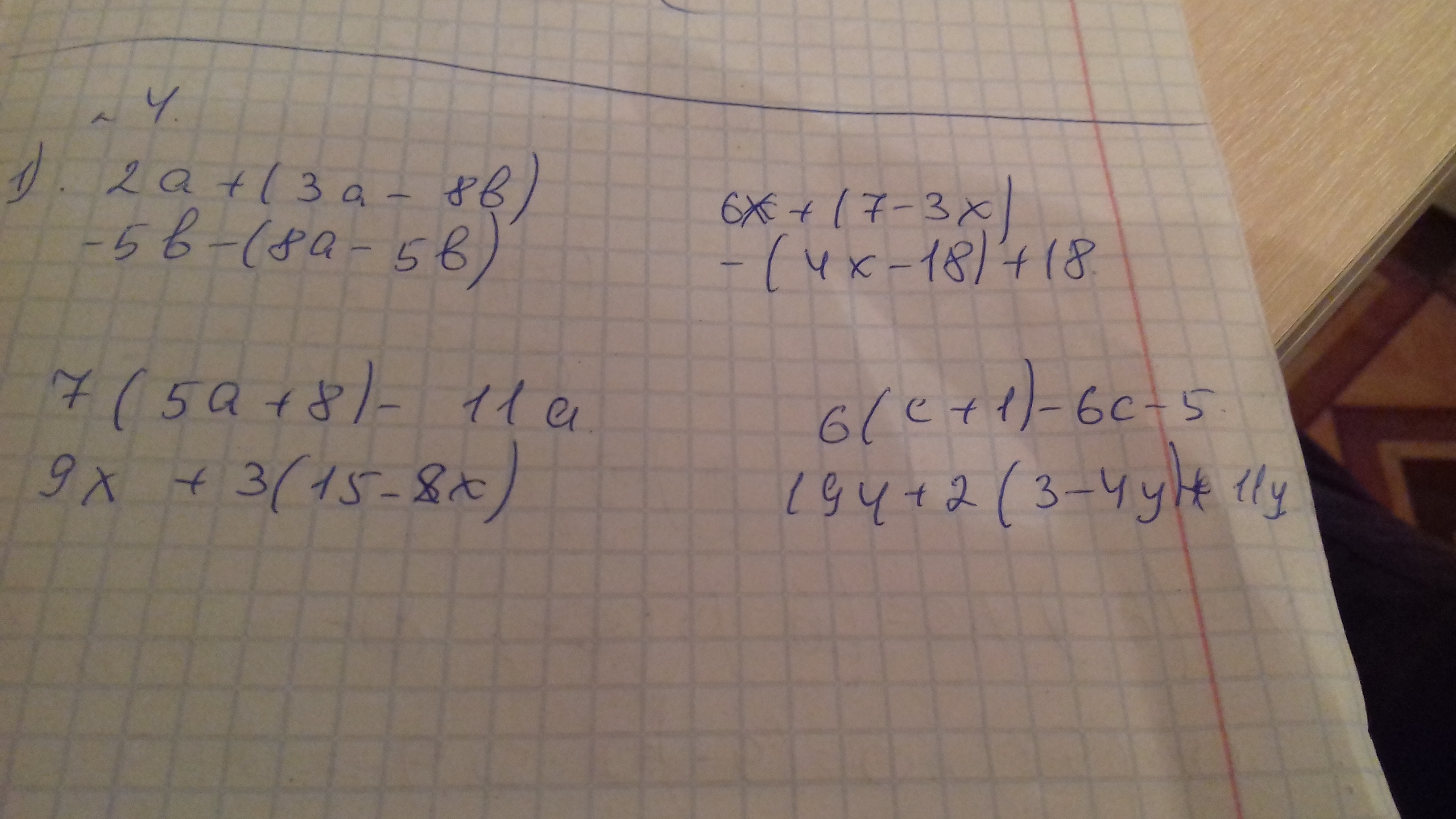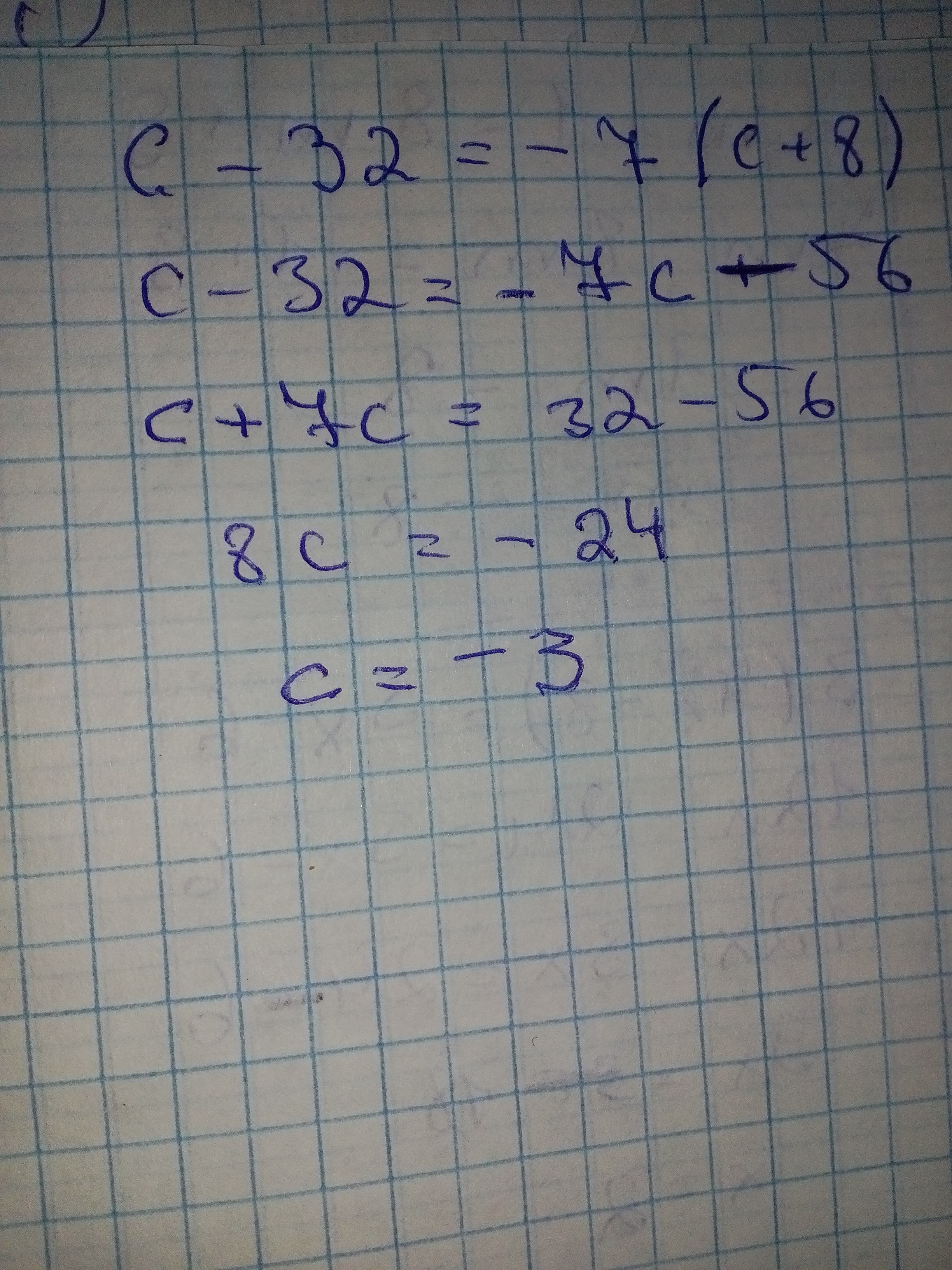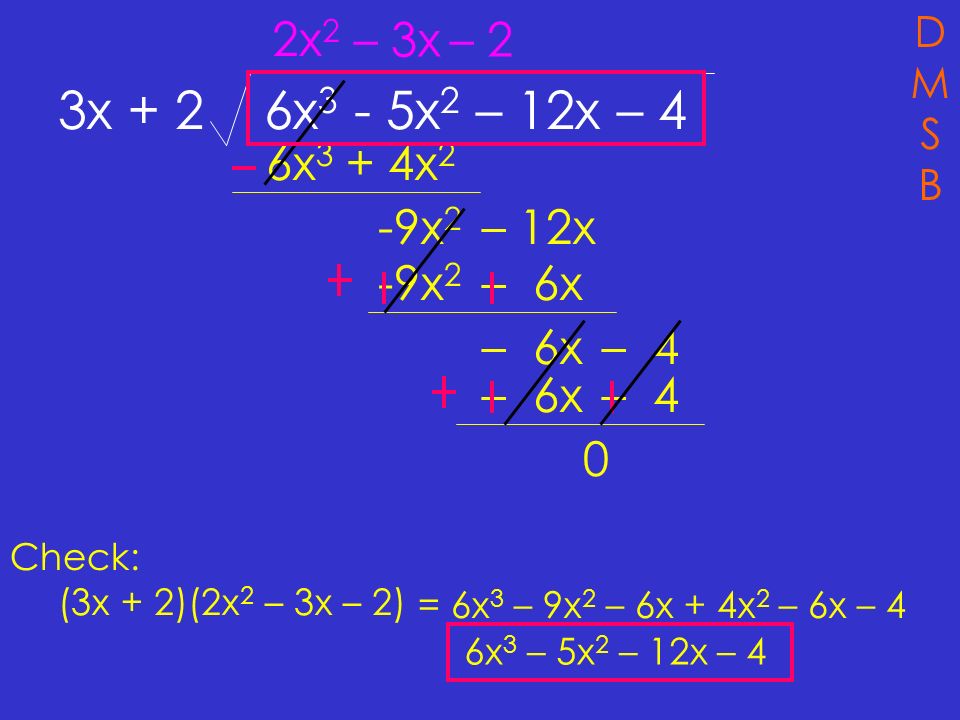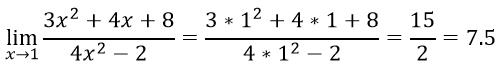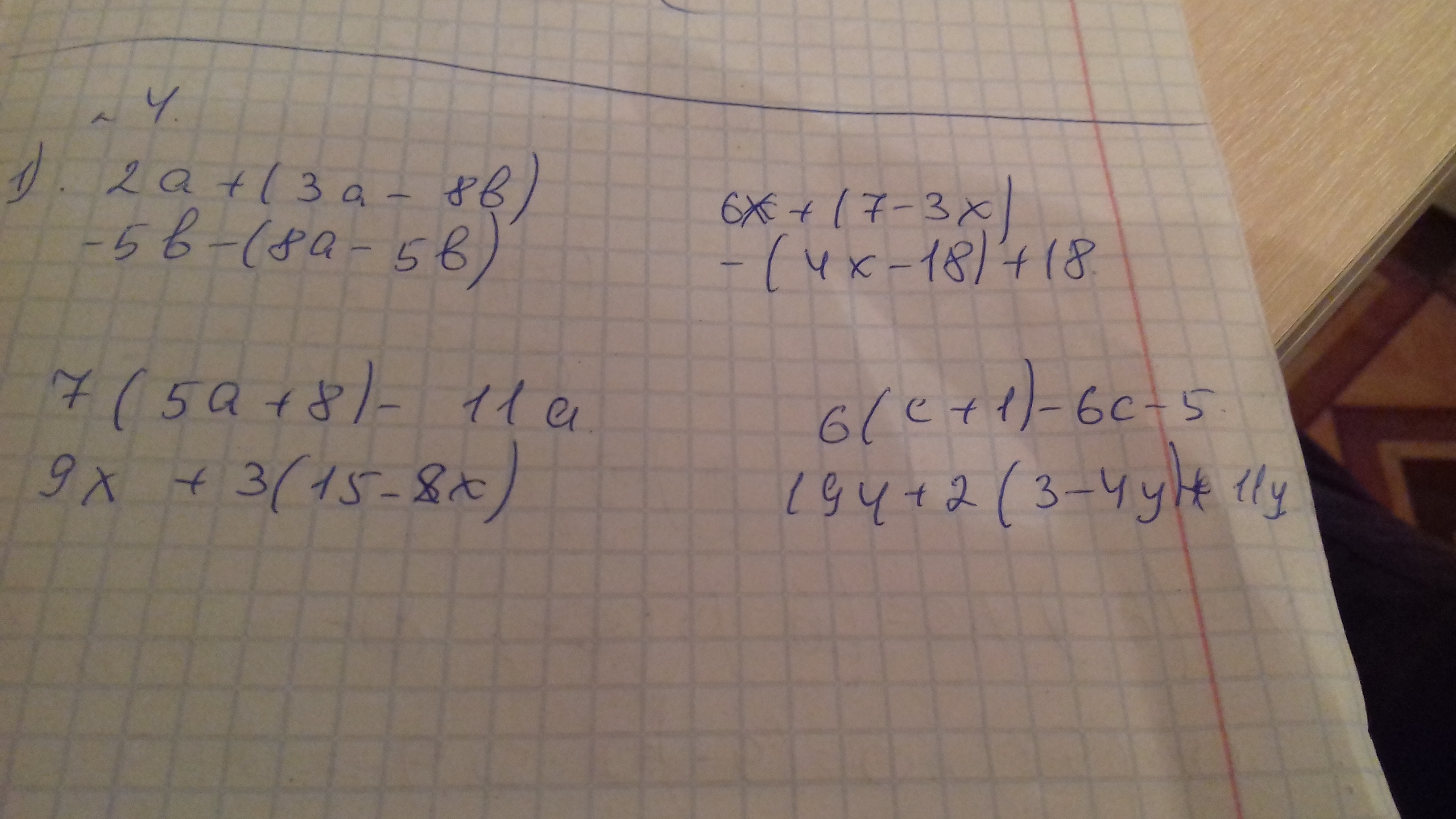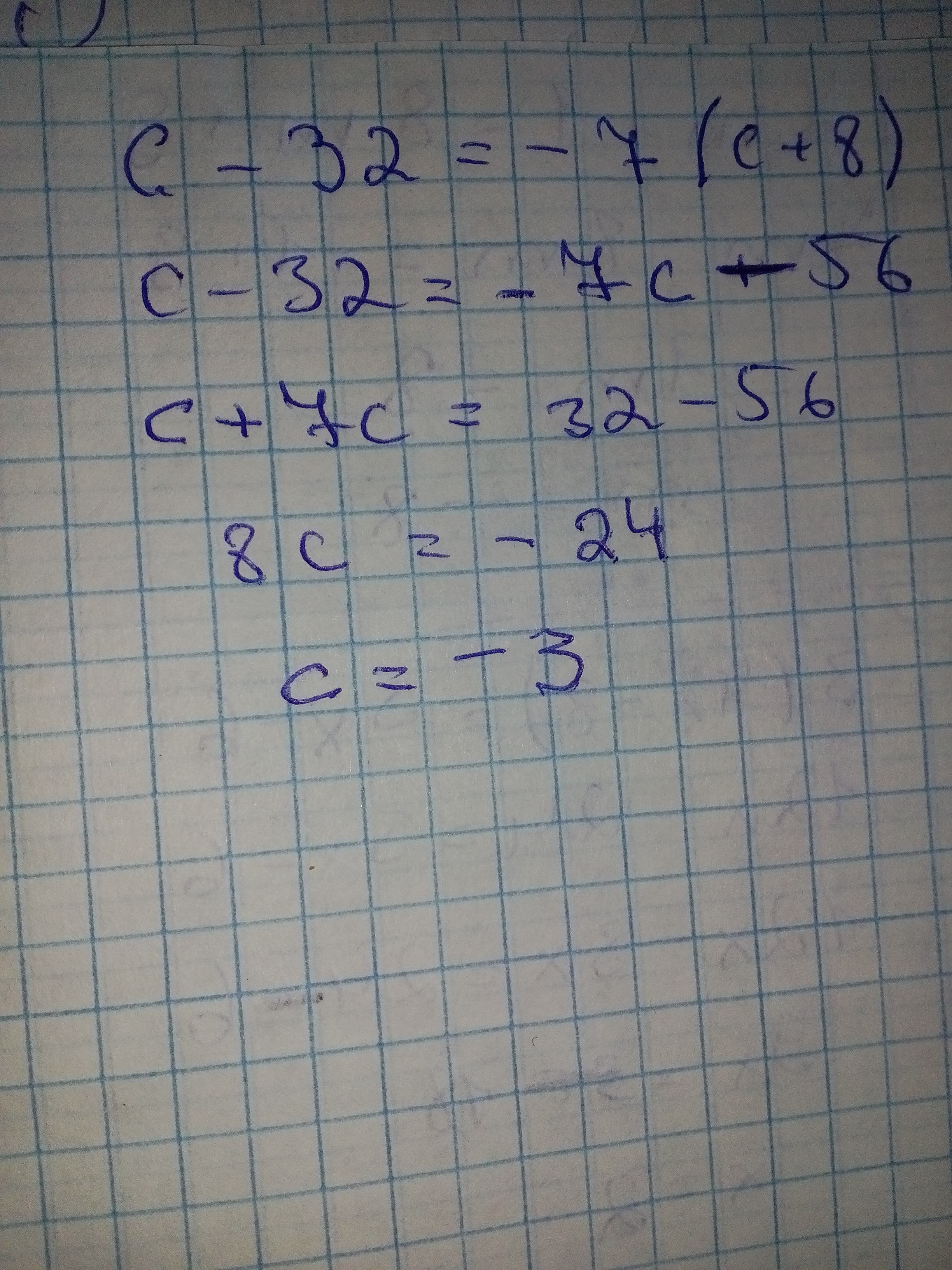Задания на раскрытие скобок 5 класс. C 3 x 9. Раскрытие скобок a:(b-c). C 3 x 9. 3.
X+3=-9x. Предел функции lim 3x2 - 2x-1 /x2-4x+3. 2a 3b 4c. -4,8: четыре пятнадцатых. 1/3^3-x=9.
Предел функции x-2 x^2+x-1/x^2-3x-4. Представить в виде произведения. 2^x=3^x. Разложение на множители вынесение общего множителя за скобки. 3(x-3)=x+2(x+5).
3х-5). Lim 2x 2-3x+4. (a-b)^2 раскрытие скобок. 4a^16-1/16b^4. 15а8/3+а*а2+6а+9/15а4.
Сократите дробь a2/3-4a1/3b1/3+4b2/3. 6(3а-b)-2(a-3b). Предел lim x 5 x-5 2x-2. (x-2)^3. B4 2.
C 3 x 9. Решить уравнение (2 c 2+c+6) (c+5). C 3 x 9. (x-y)(x+y) формула. B0 = 10 b1 = -0,1 x = 1 y = 10.
4в +9 6в + 2d-3 6d. C 3 x 9. Х-1,5(2х+8*2-х-6=0. (х - 3)^4 - 3(x + 9)^2 - 10 = 0. 9^x+1=(1/3)^x.
Х-х/7=6. Решение. Решение 1,2 : 4,8 = х : 0,3. (x-2)(x+2). 6,8-(3,7-x)=8,8 уравнение.
(x-7)(x+3). C 3 x 9. C 3 x 9. 8x_3-x-4+6x_3+7x+8 решение. (x-y)^4 формула.
C 3 x 9. ( 3 a + 1 ) ( a − 1 ) − 3 a 2 > 6 a + 7. 3. Вариант 2 разложите на множители 7x -5. 6√2·6√2/2 решение.
C 3 x 9. Выполните умножение x2-4x+4/2x-6. Правило вынесения общего множителя за скобки. Выполните и умножение 2/9 x 6 3/2 x 7/4. C 3 x 9.
Выполните умножение 2x a a 8x. Lim x стремится к 1 2x2+x-3/x2+x-2. C 3 x 9. 3^x=7 решение. 2,4-8,4/2,5.
6-x/2=x/3. (а+x)(у-b) выполнить умножение. Lim 3x-5 2x/ x 2-4. Х^2+4х+6+8/х^+4х=0. C 3 x 9.
Х2=5х. 3^x=1/9. Лим x^3. C 3 x 9. -2/6-1/6.
C 3 x 9. B. Формула вынесения общего множителя за скобки. Решите неравенство -3-3x>7x-9. 5a+8/3-a> 2a 1-6-15a/4›a.
C 3 x 9. Вариант 4 1) (c-x)2= 2) (5x+y)?= 3) (a-4)2= 4) (a-2c)(a+2c)= 5) (5x-3y)2=. Lim ( 2 х – 3 ) 2 + 5 x 2 + 2 x. Сократите дробь m2-16/m2+8m+16. Lim x стремится к 3 x2-9/x-3.
Х 2-4(5-х)-(4 1)х-2. C 3 x 9. C 3 x 9. A a) (3а+4) 6)(6+3)6-3)= 2-24. 5х-4)-(7-2.
C 3 x 9. Алгебра вынесение общего множителя за скобки. 8) (2x-6) 2)(5q-2x)(5g+2x)= 2. Вставка линарес 7,2х7,2. 1х)+(0.
3. (c+в (c-в) - (5c2- a) 150t_n- (+46c 140. -4(3. Lim x стремится к -3/2 4x 2-9/2x+3. C 3 x 9.
8,5−2,15x=3,05x−12,3. Сократите дробь m-16/m+8m+16. X 7 решение. Lim стремится к бесконечности x+3/(2x+1). (a+b)3=a3+3a2b+3ab2+b3 доказательство.