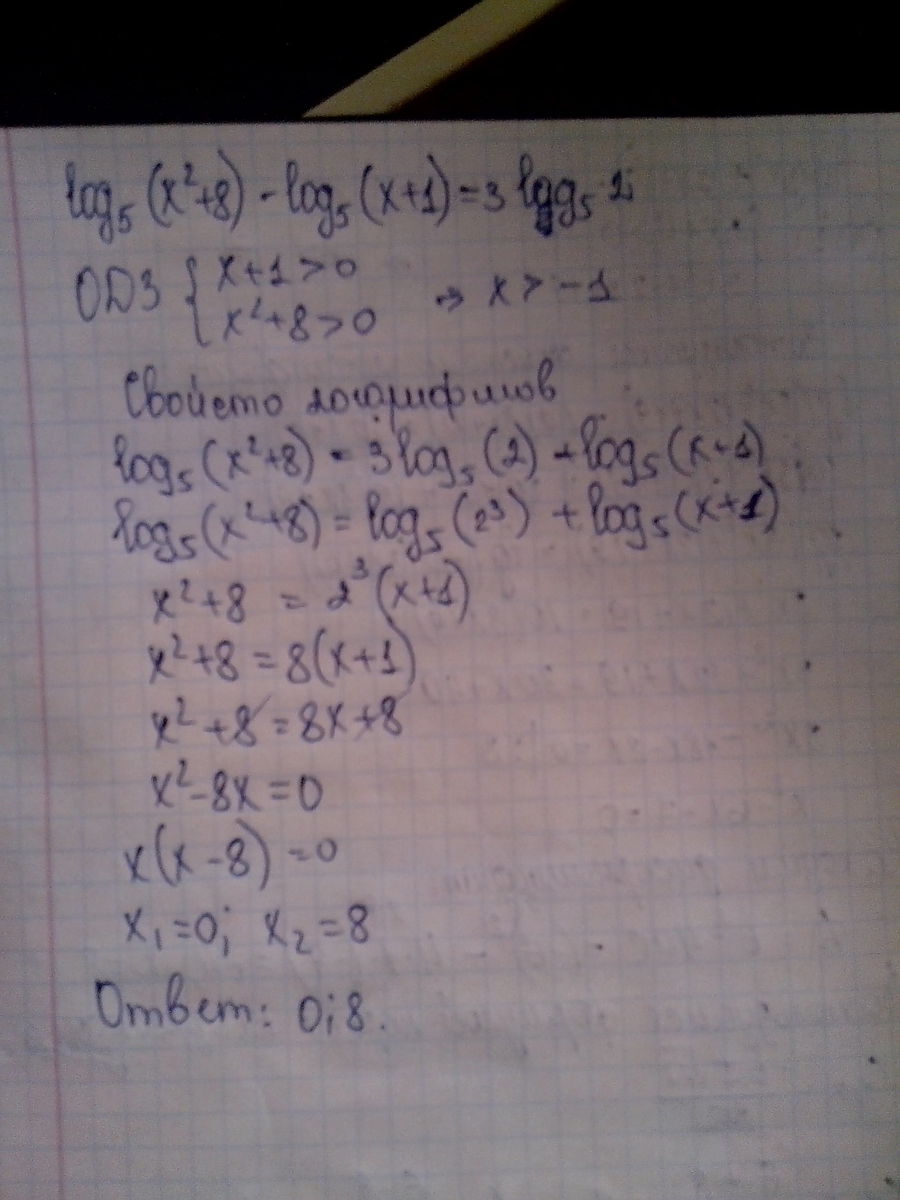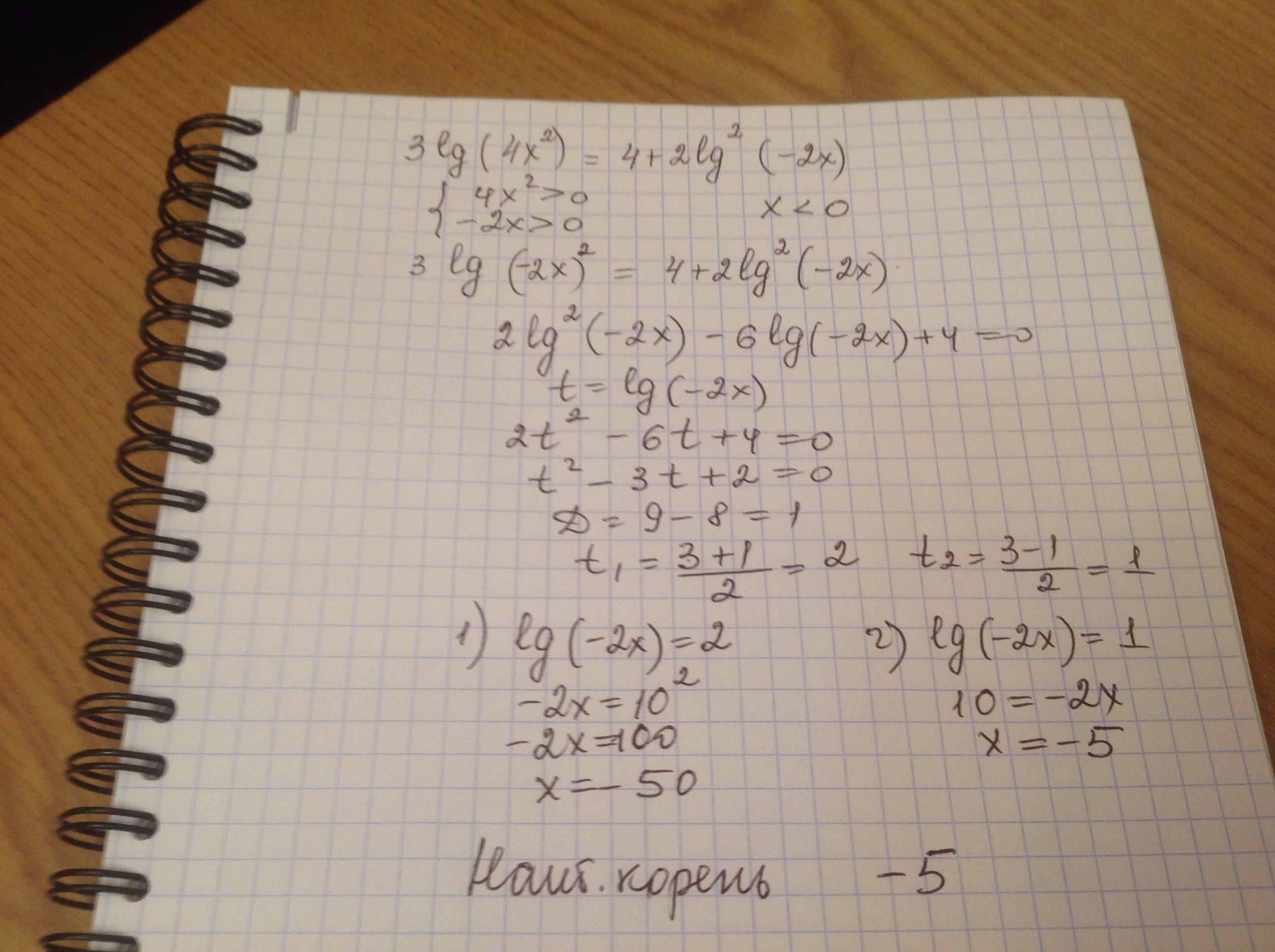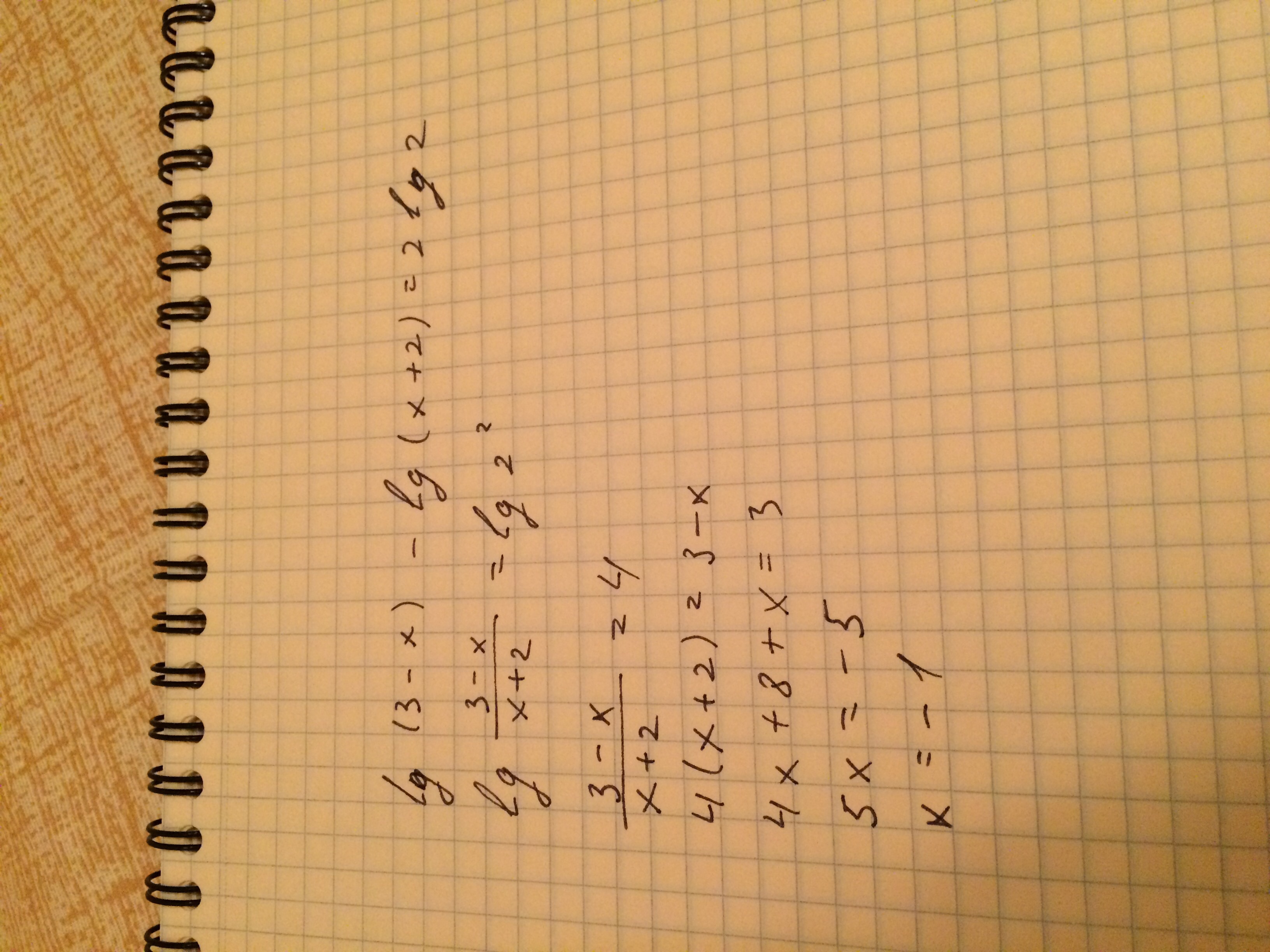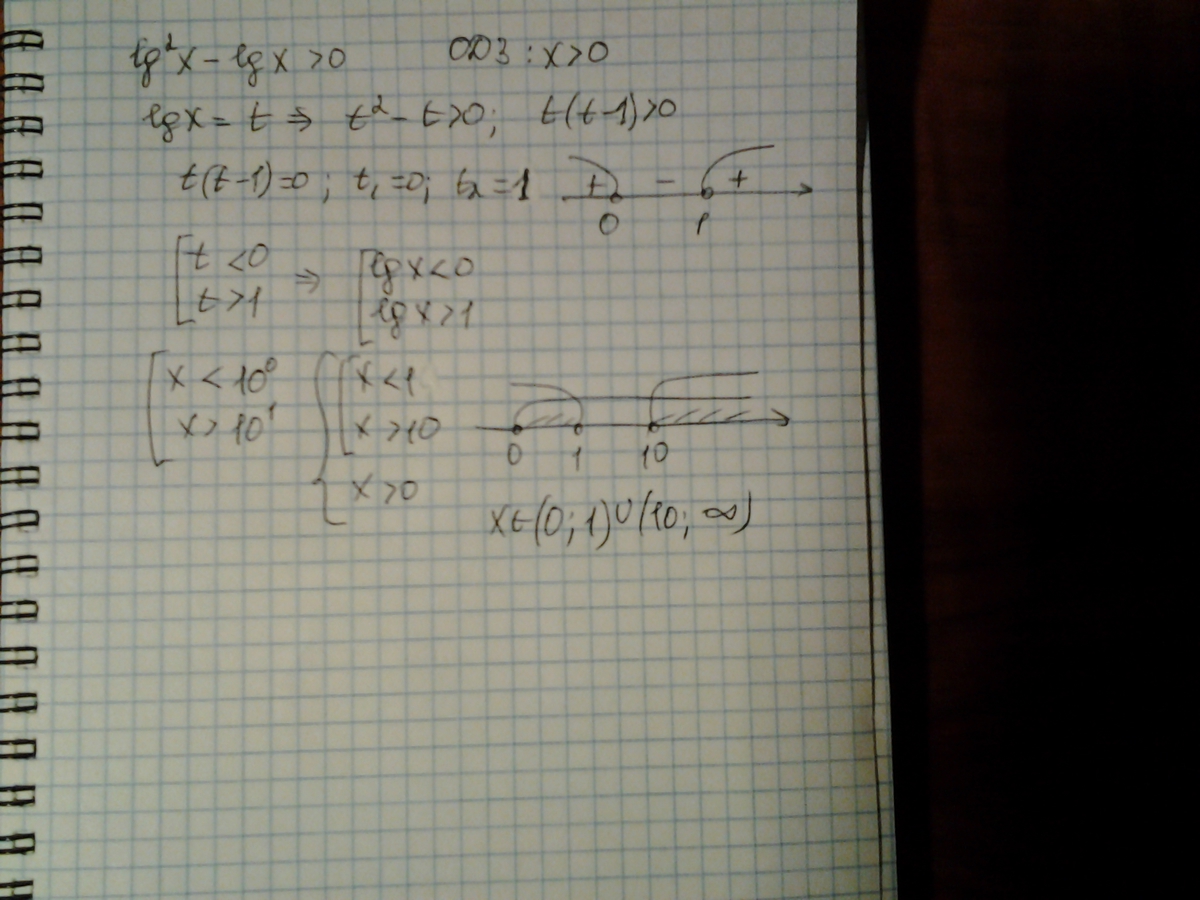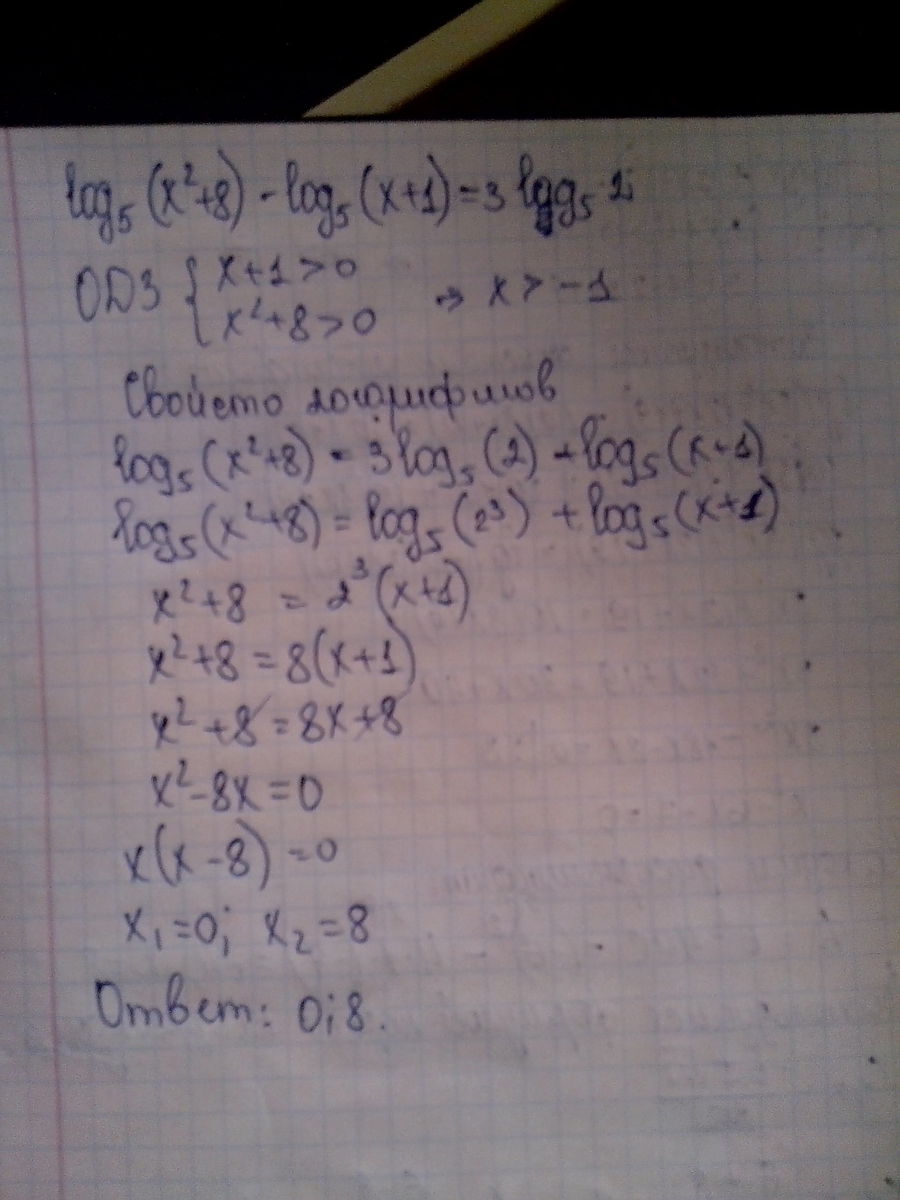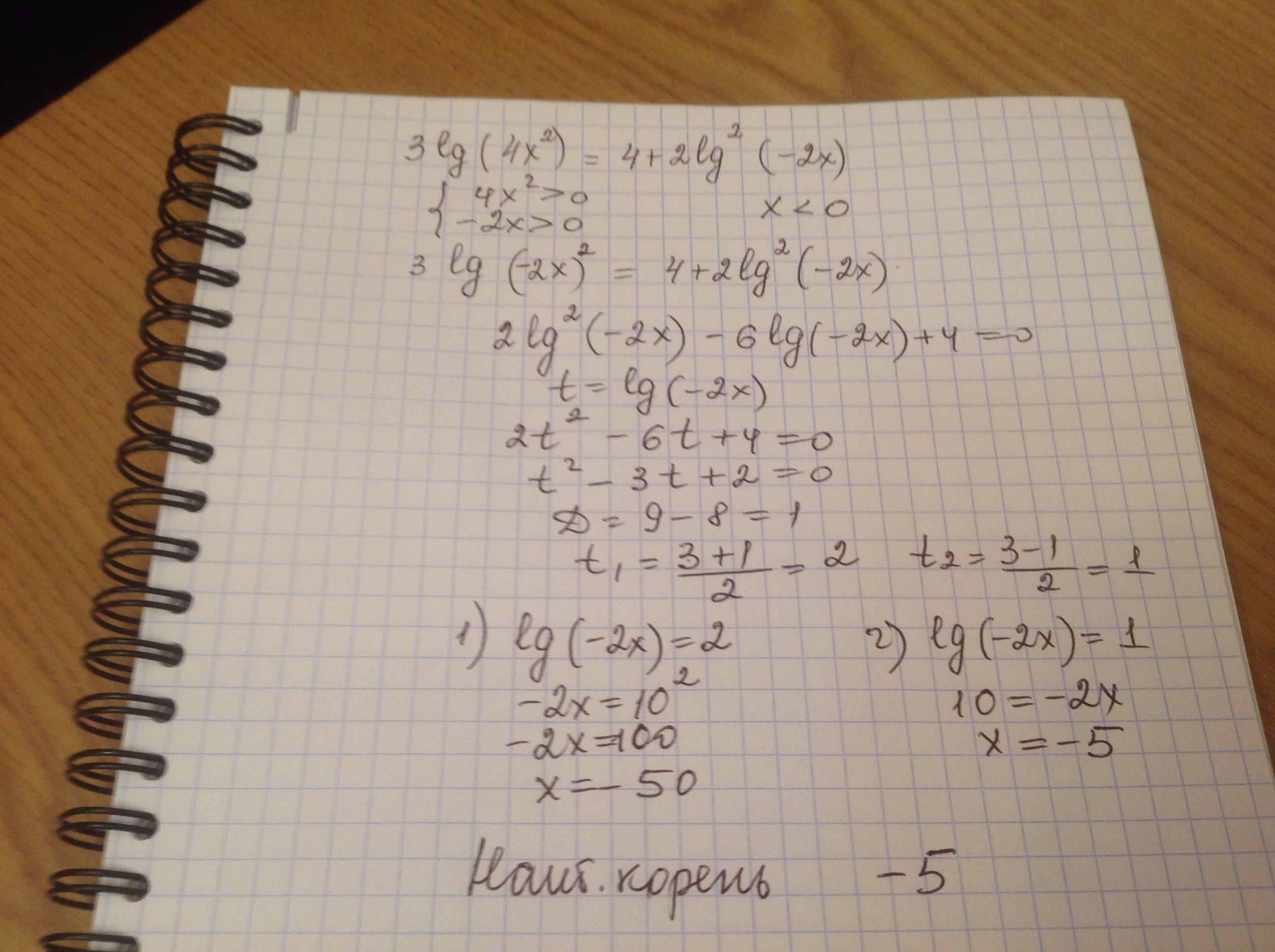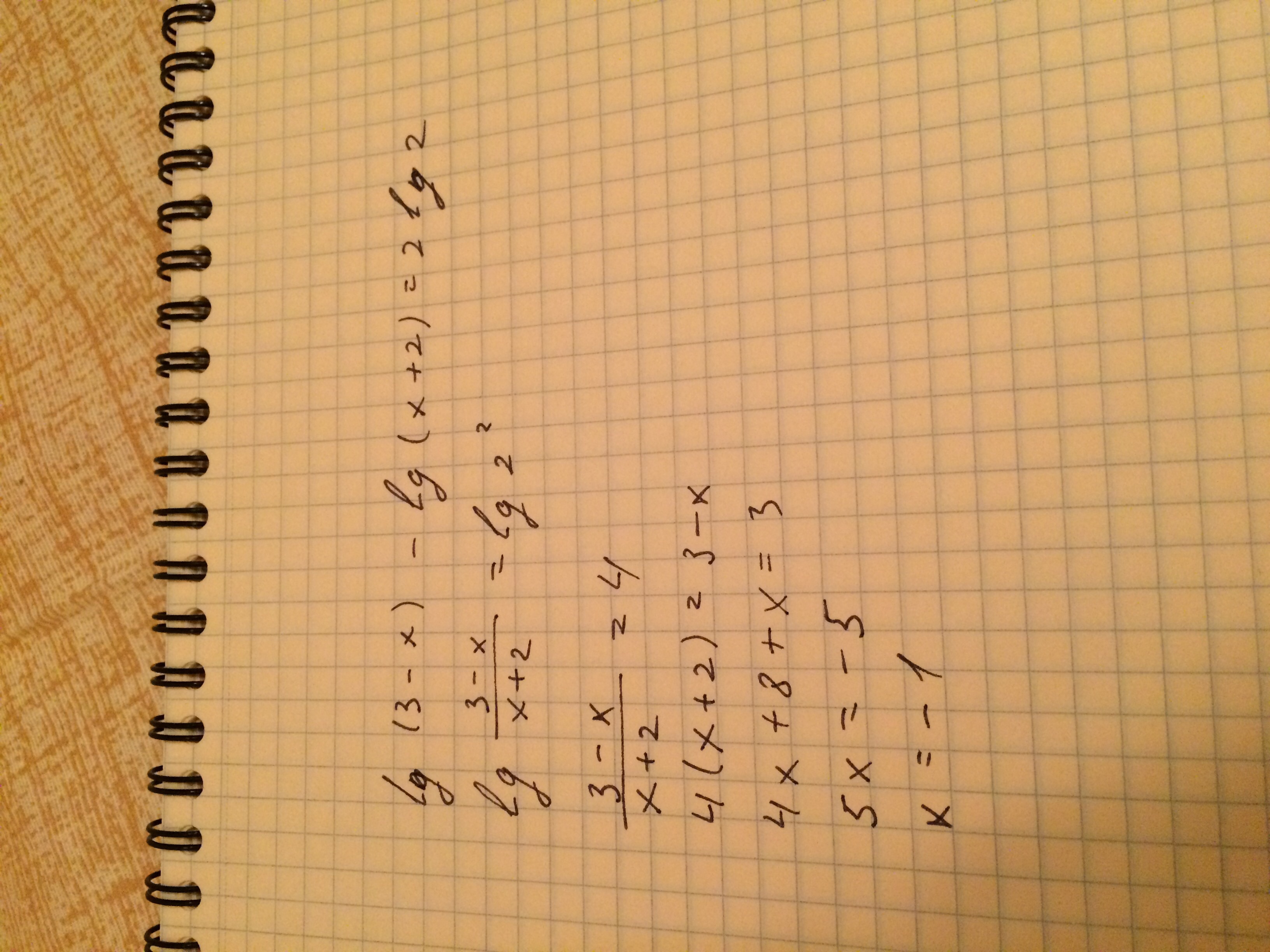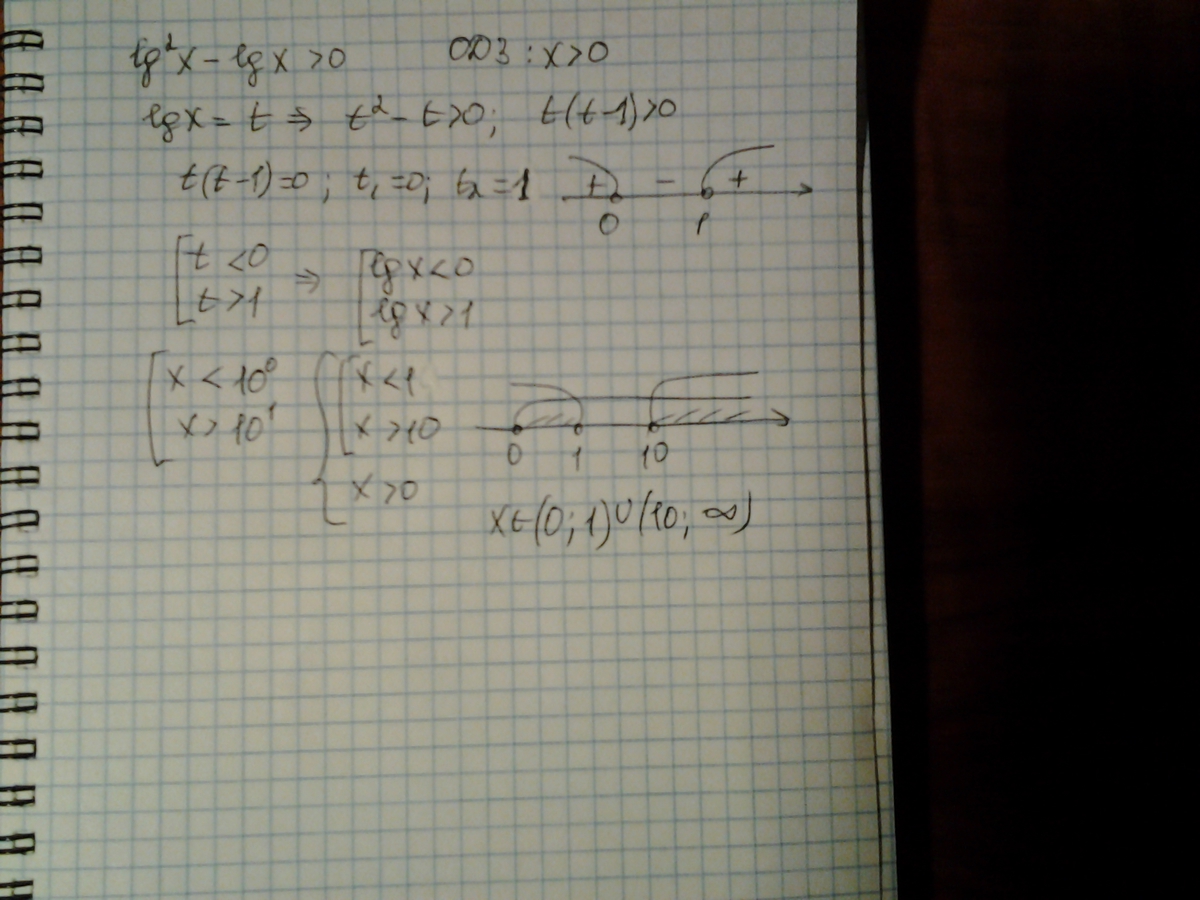Lg(x^2+2x+2)=lg30-1. Lg 2x lg x 3 lg 12x-4. Lg x2 2 lg x. Lg x 8 lg 2x 4. X2-3x+lg(x+1)=lg(x+1)+10. Lg(x^2+2x+2)=lg30-1. Lg 2x lg x 3 lg 12x-4. Lg x2 2 lg x. Lg x 8 lg 2x 4. X2-3x+lg(x+1)=lg(x+1)+10. |  Lg(x+2)+lg(x-2)=(5x+10). Lg(x^2-2)=lgx. Lg x 8 lg 2x 4. Lg(3-2x)=2lg2. Lg x 8 lg 2x 4. Lg(x+2)+lg(x-2)=(5x+10). Lg(x^2-2)=lgx. Lg x 8 lg 2x 4. Lg(3-2x)=2lg2. Lg x 8 lg 2x 4. |
 Lg x 8 lg 2x 4. Lg(x+4)-lg(x-3)=lg8. Lg x 8 lg 2x 4. Lg^2(x+2)+lg(x+2)>0. Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. Lg(x+4)-lg(x-3)=lg8. Lg x 8 lg 2x 4. Lg^2(x+2)+lg(x+2)>0. Lg x 8 lg 2x 4. |  Lg x 8 lg 2x 4. Lg(x^2-2)>= lg(4x+3). Lg x 8 lg 2x 4. Lg(x-1)+lg(x+1)=lg2. Lg 3x 4 lg 2x +1. Lg x 8 lg 2x 4. Lg(x^2-2)>= lg(4x+3). Lg x 8 lg 2x 4. Lg(x-1)+lg(x+1)=lg2. Lg 3x 4 lg 2x +1. |
 Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. Lg ( x2−2 x )=lg (2 x+12). Lg (x^2-7x+14)=lg (3x-. Lg 2x lgx 1 7/lg10x. Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. Lg ( x2−2 x )=lg (2 x+12). Lg (x^2-7x+14)=lg (3x-. Lg 2x lgx 1 7/lg10x. | 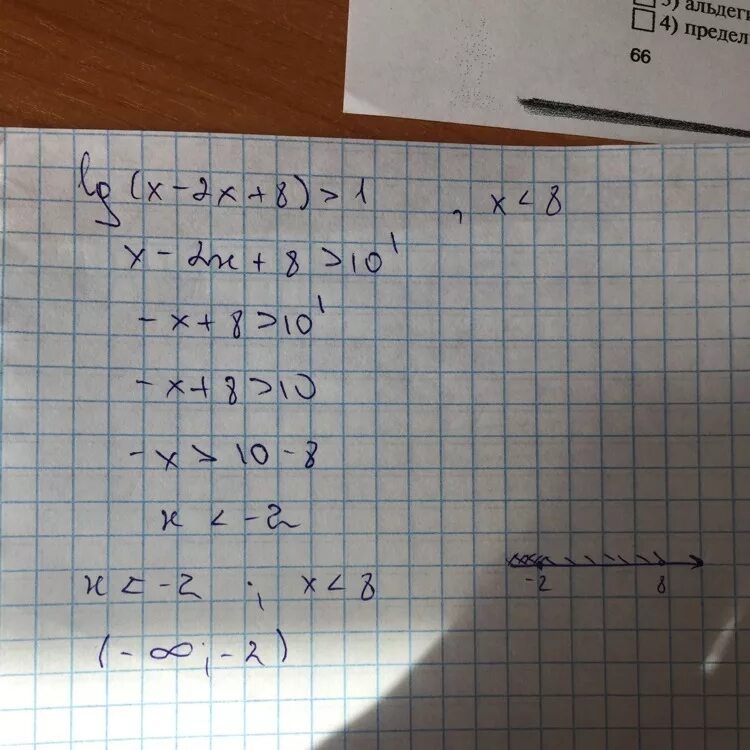 Lg4>=lg(x-2)-lg2. Lg x4 x2 6 lg x4 4x 11. Lg (x+3) = lg 5. Lg x 8 lg 2x 4. Lg(x+2)+lg(x-2)=(5x+10). Lg4>=lg(x-2)-lg2. Lg x4 x2 6 lg x4 4x 11. Lg (x+3) = lg 5. Lg x 8 lg 2x 4. Lg(x+2)+lg(x-2)=(5x+10). |
 Lg^2 x-2lg x^2+3=0. Lg (x2+2x)-lg(x+2)=0. Lg(x+2)+lg(x-2)=lg(5x+10). Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. Lg^2 x-2lg x^2+3=0. Lg (x2+2x)-lg(x+2)=0. Lg(x+2)+lg(x-2)=lg(5x+10). Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. |  б) lg(2x) + lg(x+3) = lg(12x - 4);. Lg (x2+2x)-lg(x+2)=0. Lg(x^2-2)=lgx. 2lg2(x-1)-lg(x-1)-2=0. Lg(2x-8)>lg(5+3x). б) lg(2x) + lg(x+3) = lg(12x - 4);. Lg (x2+2x)-lg(x+2)=0. Lg(x^2-2)=lgx. 2lg2(x-1)-lg(x-1)-2=0. Lg(2x-8)>lg(5+3x). |
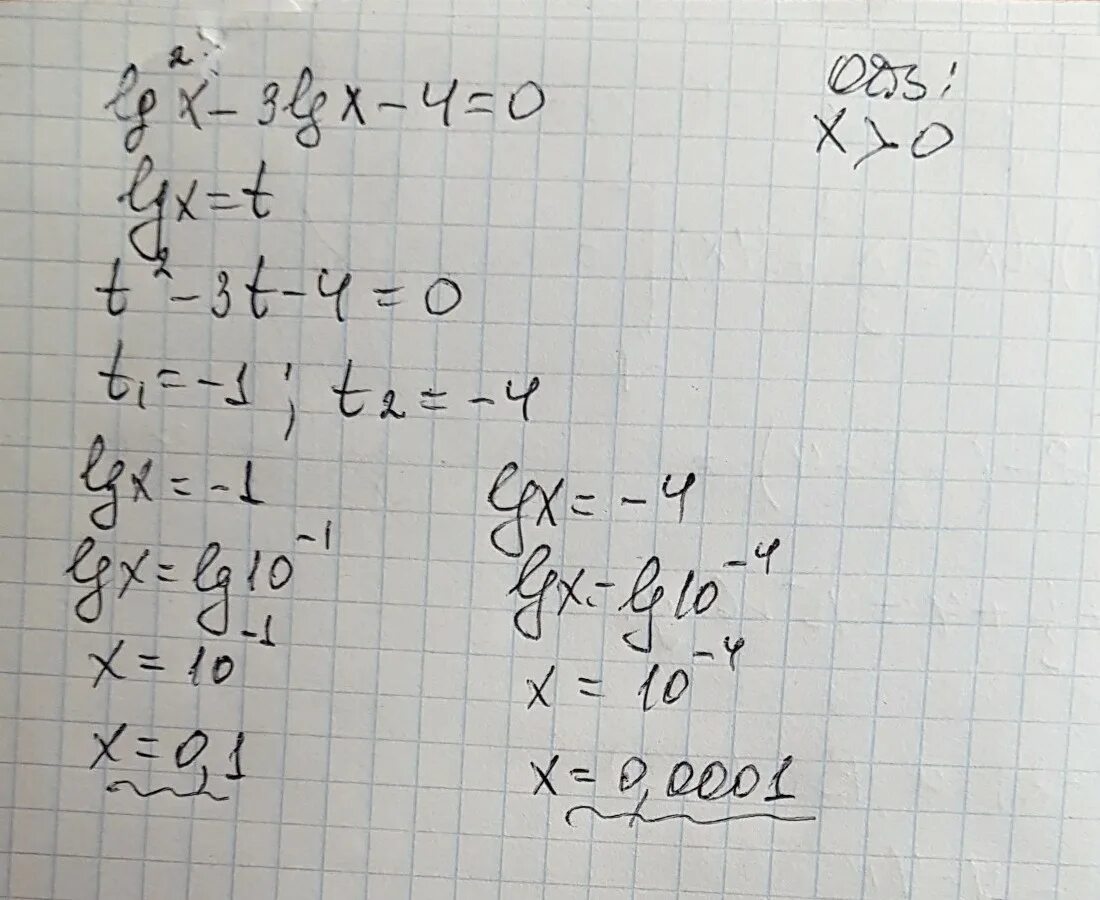 Lg(1+x)=2lg3-lg4. Lg 2 x 2 2 x 5 5 lg 2 x 5 20. Lg(x2-x)=lg(10+2x). 2lg(x+2) lg(x+4). Lg(3x-4)=2-lg20. Lg(1+x)=2lg3-lg4. Lg 2 x 2 2 x 5 5 lg 2 x 5 20. Lg(x2-x)=lg(10+2x). 2lg(x+2) lg(x+4). Lg(3x-4)=2-lg20. |  4-lg 2x 3lgx. Lg(𝑥2 − 2𝑥) + 1 = lg(30);. X2-3x+lg(x+1)=lg(x+1)+10. Lg x-log2 5x-1 lg x. 2 lg x 2-4 x+2 lg2. 4-lg 2x 3lgx. Lg(𝑥2 − 2𝑥) + 1 = lg(30);. X2-3x+lg(x+1)=lg(x+1)+10. Lg x-log2 5x-1 lg x. 2 lg x 2-4 x+2 lg2. |
 Lg^2〖x^2 〗-lg〖x^5 〗+1≥0. Lg 2 x 3 lg x 4. Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. Lg(x^2-2)=-lg1/x. Lg^2〖x^2 〗-lg〖x^5 〗+1≥0. Lg 2 x 3 lg x 4. Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. Lg(x^2-2)=-lg1/x. |  1. Lg(x^2+2x-7)=lg(x-1). ((x2+x)lg(x2+2x–2))/|x–1| ≥ (lg(–x2–2x+2)2)/(x–1). 1/(1+lg x). Lg x-4/x-2 lgx. 1. Lg(x^2+2x-7)=lg(x-1). ((x2+x)lg(x2+2x–2))/|x–1| ≥ (lg(–x2–2x+2)2)/(x–1). 1/(1+lg x). Lg x-4/x-2 lgx. |
 Lg(x^2+2x-3)=lg(2x^2-2). Lg x 8 lg 2x 4. Lg(x+2)=1+lgx. Lg(x^2+2x-7)=lg(x-1). Lg x 8 lg 2x 4. Lg(x^2+2x-3)=lg(2x^2-2). Lg x 8 lg 2x 4. Lg(x+2)=1+lgx. Lg(x^2+2x-7)=lg(x-1). Lg x 8 lg 2x 4. | 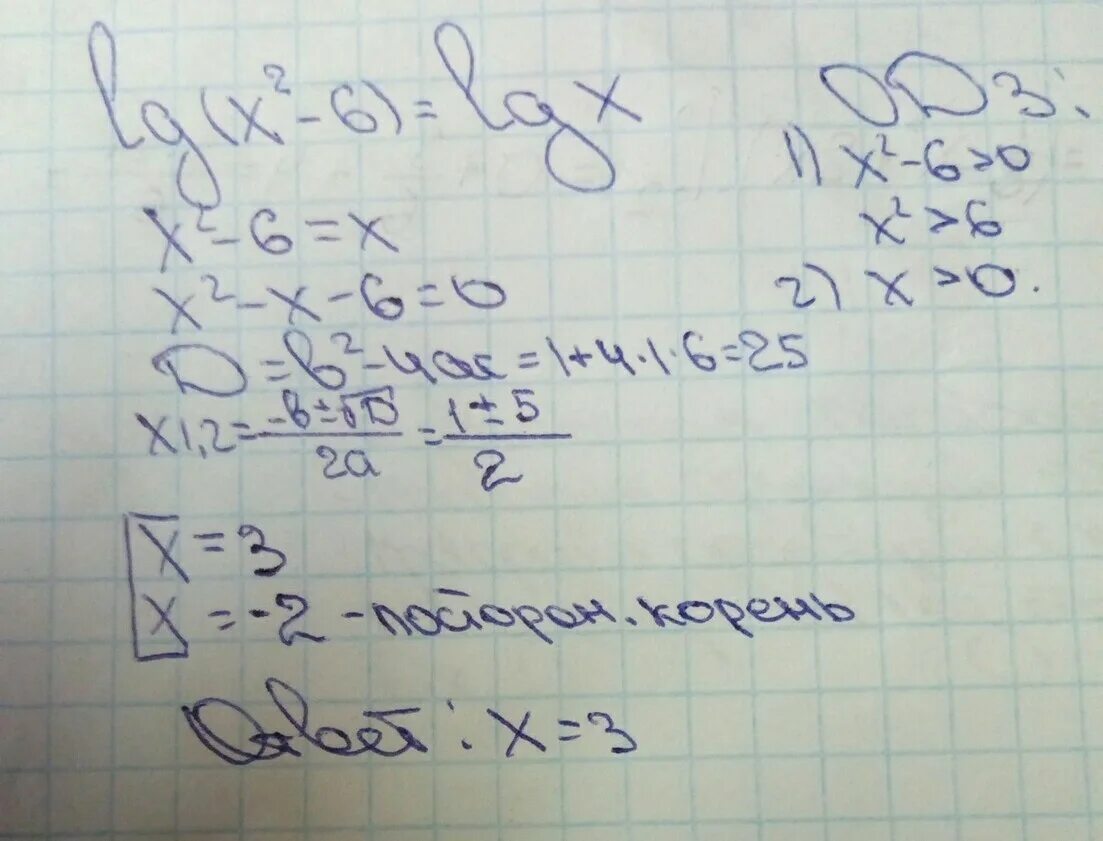 Lg x 8 lg 2x 4. Lg x2 2x lg 30-1. Lg x 4-x 2-3 lg x 4+3x-7. Lg(x-3)+lg(x-2)=lg2. Lg2(x+2)+lg(x-2). Lg x 8 lg 2x 4. Lg x2 2x lg 30-1. Lg x 4-x 2-3 lg x 4+3x-7. Lg(x-3)+lg(x-2)=lg2. Lg2(x+2)+lg(x-2). |
 Lg 2x 3 lg x+1. Lg 2 x 3 lg x 4. Lg^2 x-lg x-2=0. Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. Lg 2x 3 lg x+1. Lg 2 x 3 lg x 4. Lg^2 x-lg x-2=0. Lg x 8 lg 2x 4. Lg x 8 lg 2x 4. | 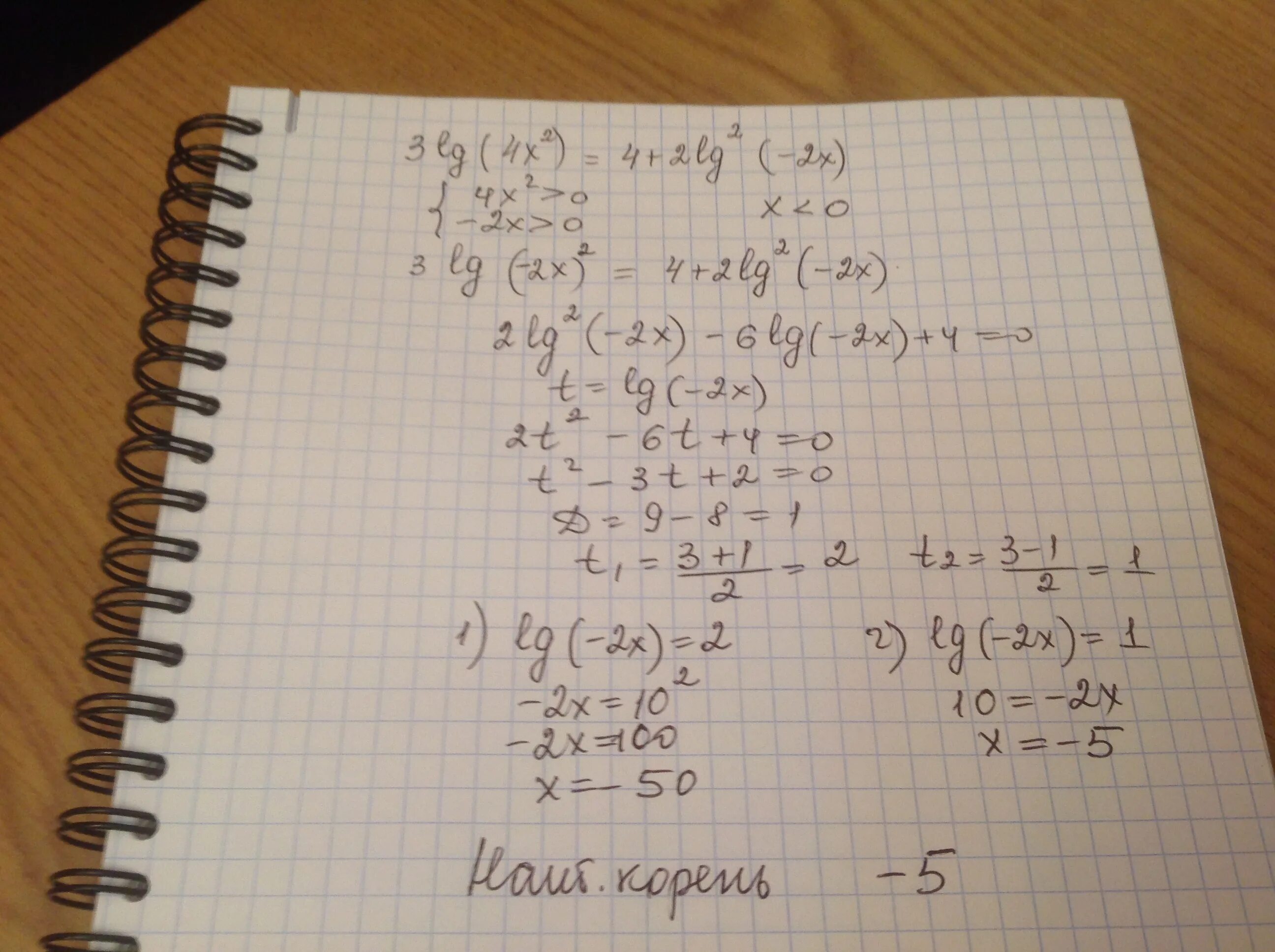 Lg^2 x-lg x-2=0. 3lg 2x-8/lg 2x-4 2. Lg^2 x-lg x-2=0. 3lg 2x-8/lg 2x-4 2. |
 Lg x 8 lg 2x 4 Lg x 8 lg 2x 4 |  Lg x 8 lg 2x 4 Lg x 8 lg 2x 4 |
 Lg x 8 lg 2x 4 Lg x 8 lg 2x 4 |  Lg x 8 lg 2x 4 Lg x 8 lg 2x 4 |