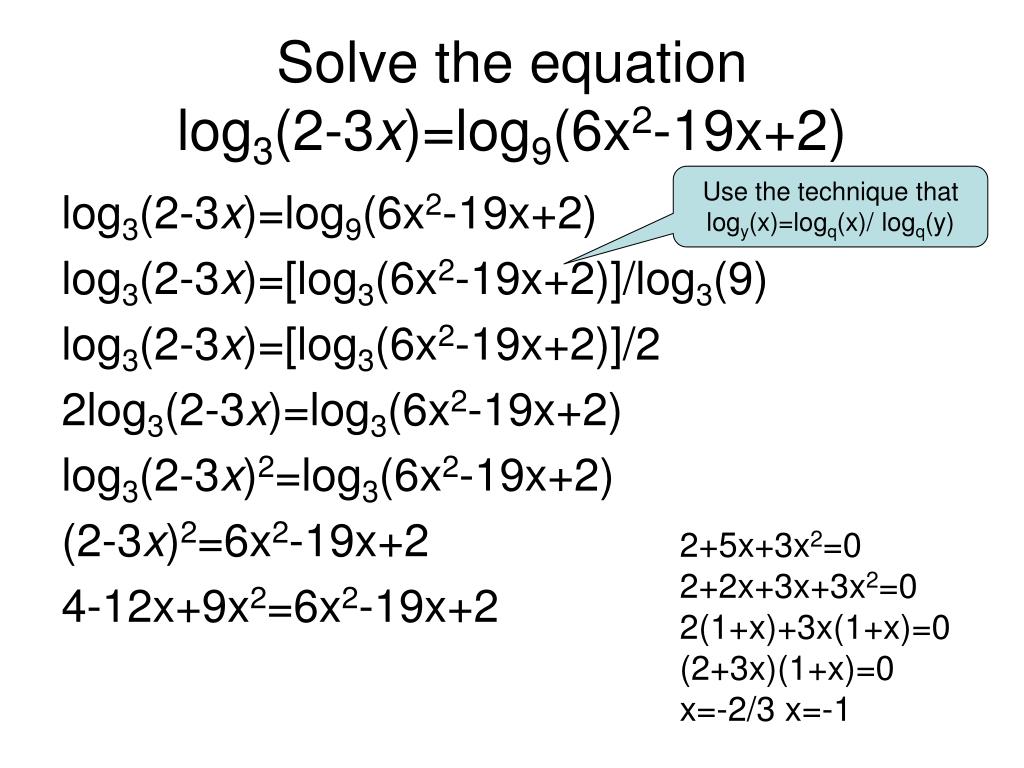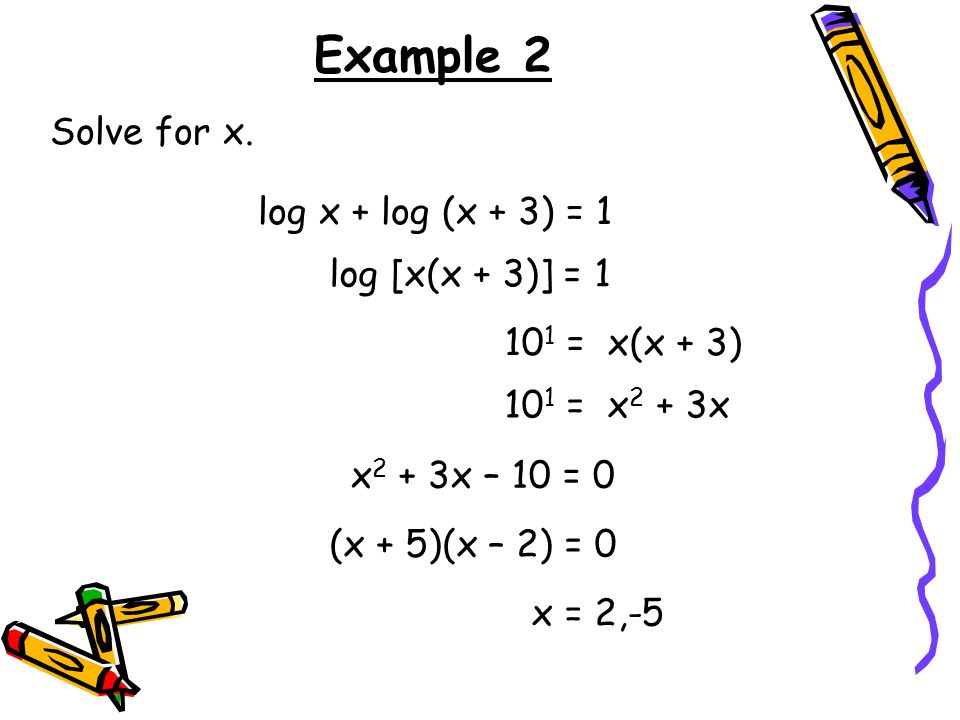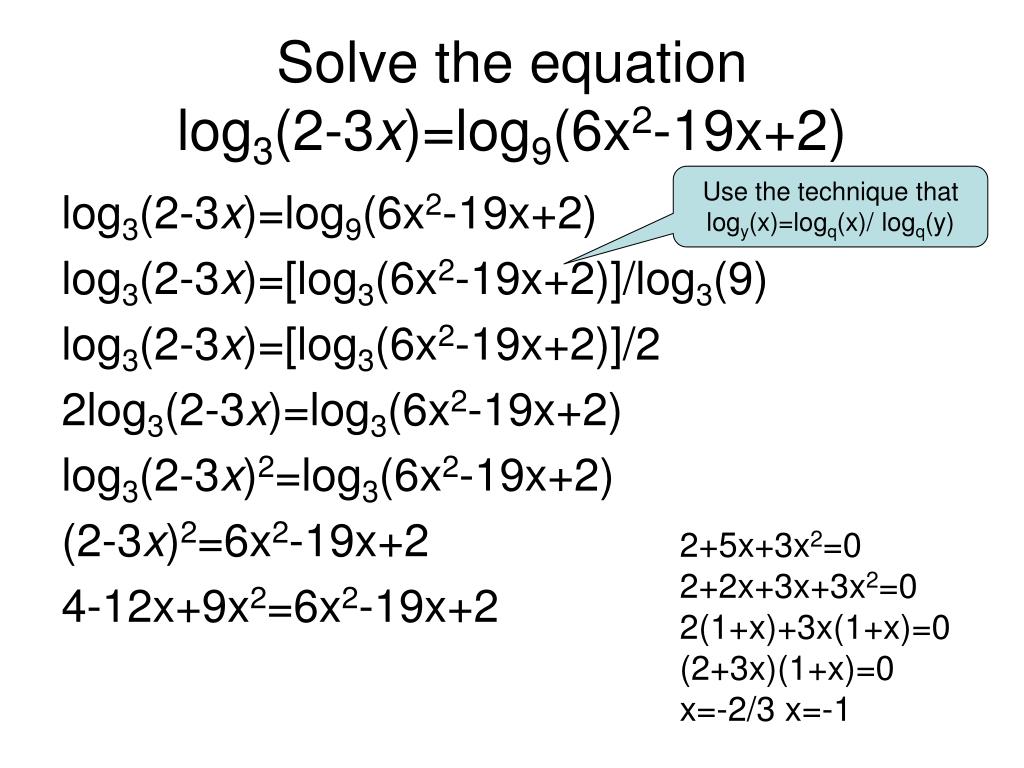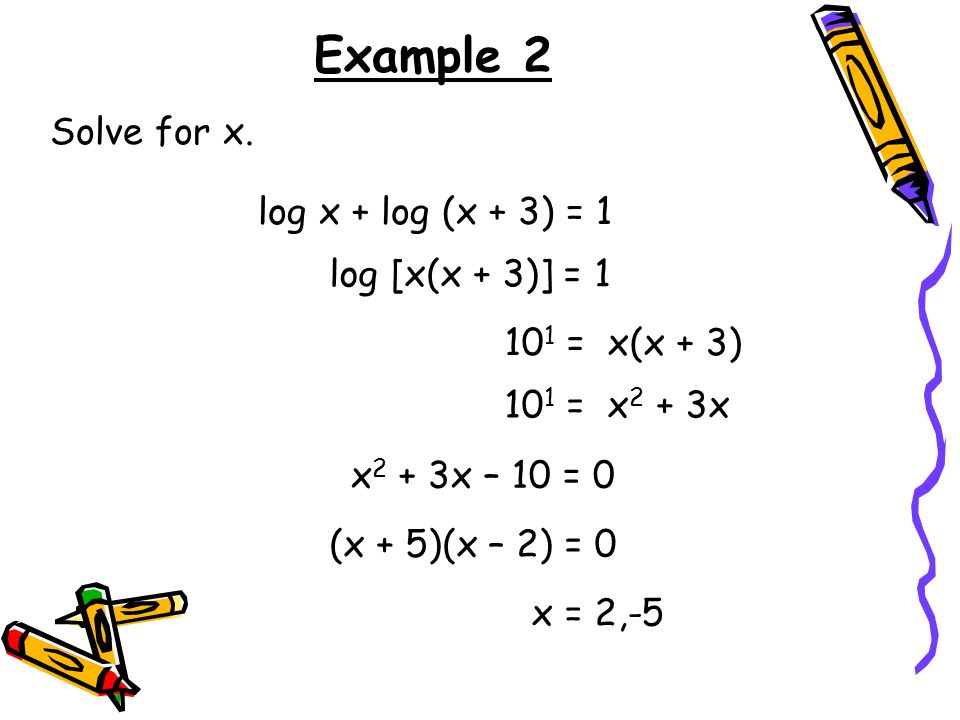Удиви меня

Log2 х 3 2

Log2 х 3 2. Лог 1/3 х2 -2 -1. Log4(2х-3)= 1. 1. Корень уравнения log2 (5+x)=2.
Log2 х 3 2. Лог 1/3 х2 -2 -1. Log4(2х-3)= 1. 1. Корень уравнения log2 (5+x)=2.
Log3(х-3) 1. Метод введения новой переменной логарифм. Log 3,5х+0,5(1,5х+3)> 1 x-1. 3 log2 x+1. Log2 х 3 2.
Log3(х-3) 1. Метод введения новой переменной логарифм. Log 3,5х+0,5(1,5х+3)> 1 x-1. 3 log2 x+1. Log2 х 3 2.
Log4(x-1)-log 4 (2х-2)=0. Лог2(2х)+лог(х+3)= лог. Лог 2 3 лог 3 4. Решите уравнение log3 8+7x log3 (3+x) +1. Log_2⁡ (3х−2)=4.
Log4(x-1)-log 4 (2х-2)=0. Лог2(2х)+лог(х+3)= лог. Лог 2 3 лог 3 4. Решите уравнение log3 8+7x log3 (3+x) +1. Log_2⁡ (3х−2)=4.
Решение уравнение log3(x-2)=2. Log2 х 3 2. Решение логарифмических уравнений 1/3 log 3 (5x-1) - log 3 (x+1) = 0. Лог2 (3х-1)>лог2(2-7х). Log2 х 3 2.
Решение уравнение log3(x-2)=2. Log2 х 3 2. Решение логарифмических уравнений 1/3 log 3 (5x-1) - log 3 (x+1) = 0. Лог2 (3х-1)>лог2(2-7х). Log2 х 3 2.
Log2 х 3 2. Логарифмические уравнения log2/3 + log3. Лог 3 6 5х лог 3 4-5x +2. Log2 х 3 2. Log2 (х– 1)≤ – 4.
Log2 х 3 2. Логарифмические уравнения log2/3 + log3. Лог 3 6 5х лог 3 4-5x +2. Log2 х 3 2. Log2 (х– 1)≤ – 4.
Решите неравенство log. Log2 х 3 2. Решение log3(x-2)=log3(2-x). Решения логарифмических уравнений log2 x=1. Log9 x 7 2 log81 x 3 4+log3 x 3 3x.
Решите неравенство log. Log2 х 3 2. Решение log3(x-2)=log3(2-x). Решения логарифмических уравнений log2 x=1. Log9 x 7 2 log81 x 3 4+log3 x 3 3x.
Log2(2x-2). Решить уравнение log. Log2 х 3 2. 2log2 x-1/x+1. Log2 х 3 2.
Log2(2x-2). Решить уравнение log. Log2 х 3 2. 2log2 x-1/x+1. Log2 х 3 2.
Лог 0,5(2х-3) =1. Log3. Log2 (x2-x+3) >3. Лог 3 6+5х лог 3 4-5х +2. Log_3⁡〖1/х〗 +log_3⁡〖(х^2 〗+3х-9)≤log_3⁡〖(х^2 〗+3х +1/х – 9).
Лог 0,5(2х-3) =1. Log3. Log2 (x2-x+3) >3. Лог 3 6+5х лог 3 4-5х +2. Log_3⁡〖1/х〗 +log_3⁡〖(х^2 〗+3х-9)≤log_3⁡〖(х^2 〗+3х +1/х – 9).
Log 2 x решить решить неравенство. 3log3 2. Log_3⁡〖(2х-1)-log_3⁡〖х=2〗. Log 3,5х+0,5(1,5х+3)> 1 x-1. Log2 х 3 2.
Log 2 x решить решить неравенство. 3log3 2. Log_3⁡〖(2х-1)-log_3⁡〖х=2〗. Log 3,5х+0,5(1,5х+3)> 1 x-1. Log2 х 3 2.
Log2 х 3 2. Log3 2 log3 2 log2 6 log3 6. Решить неравенство log(2 - x) 2. Log2 2 𝑥 − 2 log2 𝑥 − 3 = 0. Лог 1/2 2х+5 -3.
Log2 х 3 2. Log3 2 log3 2 log2 6 log3 6. Решить неравенство log(2 - x) 2. Log2 2 𝑥 − 2 log2 𝑥 − 3 = 0. Лог 1/2 2х+5 -3.
Логарифм 7 (х+6) = лог 9(6х-9). Log2 х 3 2. Лог5 (3-х)=2. Решите уравнение: log3 (3-2х)=3. Лог5 5-х=лог5 3.
Логарифм 7 (х+6) = лог 9(6х-9). Log2 х 3 2. Лог5 (3-х)=2. Решите уравнение: log3 (3-2х)=3. Лог5 5-х=лог5 3.
Log2 х 3 2. Log1 2 3 5х 3. Log2log 2 x^3+8 log 2 x+2 + 2log2 4-x. Лог 4 2^х - 1 / х - 1. Решение log уравнений.
Log2 х 3 2. Log1 2 3 5х 3. Log2log 2 x^3+8 log 2 x+2 + 2log2 4-x. Лог 4 2^х - 1 / х - 1. Решение log уравнений.
Log 0,4 (2x3 + х2 - 5х - 7) = log 0,4 (х3 - 2х2 - 2х + 7). Log4(x-1)-log 4 (2х-2)=0. 2лог2(х) 3лог3х. Решить уравнение log. Log2 3.
Log 0,4 (2x3 + х2 - 5х - 7) = log 0,4 (х3 - 2х2 - 2х + 7). Log4(x-1)-log 4 (2х-2)=0. 2лог2(х) 3лог3х. Решить уравнение log. Log2 3.
Log2(log2x)=1. Log(3х-2)=2. Log2 (х2-9) - 9log2(х2-9). Log2 х 3 2. Log2x>1.
Log2(log2x)=1. Log(3х-2)=2. Log2 (х2-9) - 9log2(х2-9). Log2 х 3 2. Log2x>1.
Лог 3 х2-х-3 лог 3 2х2+х-3. Лог 3 х2-х-3 лог 3 2х2+х-3. 2лог5(х2-5х)/лог5(х2). 2 log2 3-3. 2лог2(х) 3лог3х.
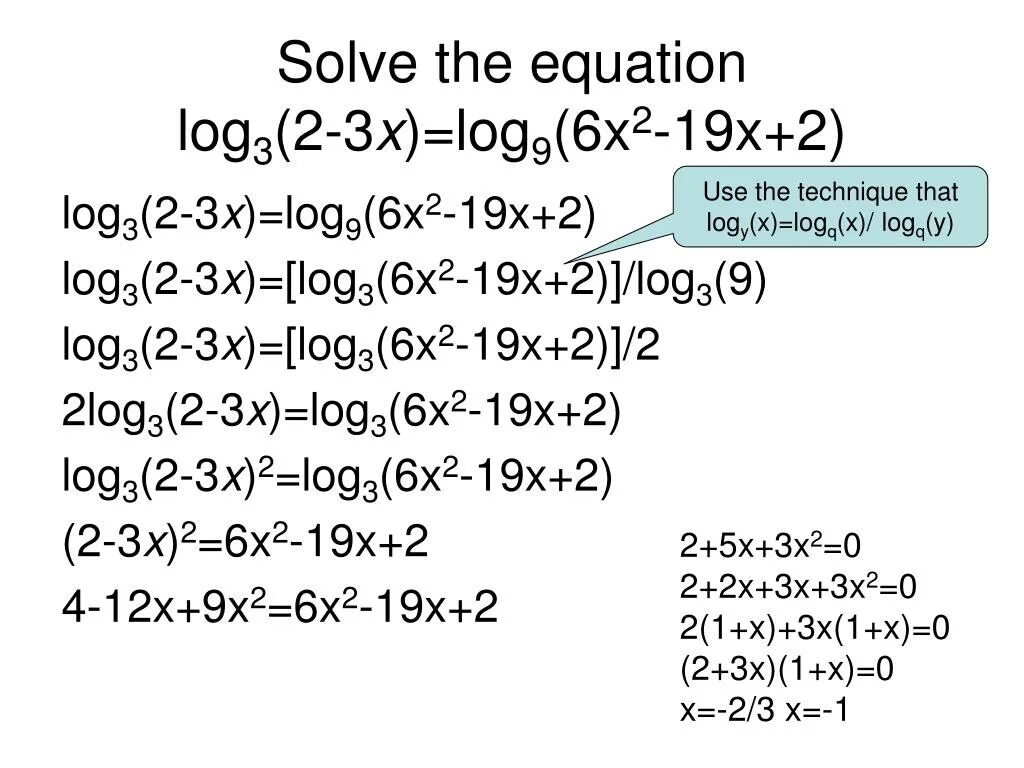Лог 3 х2-х-3 лог 3 2х2+х-3. Лог 3 х2-х-3 лог 3 2х2+х-3. 2лог5(х2-5х)/лог5(х2). 2 log2 3-3. 2лог2(х) 3лог3х.
2 log2 3-3. Решить уравнение log. Решение логарифмических уравнений. Решить уравнение лог. Решение лог уравнений.
2 log2 3-3. Решить уравнение log. Решение логарифмических уравнений. Решить уравнение лог. Решение лог уравнений.
Log2 х 3 2. 3 2. Логарифмические уравнения. Лог 3 х2-х-3 лог 3 2х2+х-3. Log2 х 3 2.
Log2 х 3 2. 3 2. Логарифмические уравнения. Лог 3 х2-х-3 лог 3 2х2+х-3. Log2 х 3 2.
Log2 х 3 2. Метод введения новой переменной логарифмические уравнения. Лог5 5-х=лог5 3. Log2(x-3)<1. Лог 3/4 1/4х-1 2.
Log2 х 3 2. Метод введения новой переменной логарифмические уравнения. Лог5 5-х=лог5 3. Log2(x-3)<1. Лог 3/4 1/4х-1 2.
Log2 х 3 2. Log2 х 3 2. Логарифмические уравнения log12 (x^2-x)=1. Log2 х 3 2. Log2(х+3)=−1.
Log2 х 3 2. Log2 х 3 2. Логарифмические уравнения log12 (x^2-x)=1. Log2 х 3 2. Log2(х+3)=−1.
Log0,5 (2х-4)=-1. Решение log5. Введение новой переменной логарифмических уравнений. Log_1/3(x+2)-log_9(x+2)=>-3/2. Лог2(2х)+лог(х+3)= лог.
Log0,5 (2х-4)=-1. Решение log5. Введение новой переменной логарифмических уравнений. Log_1/3(x+2)-log_9(x+2)=>-3/2. Лог2(2х)+лог(х+3)= лог.