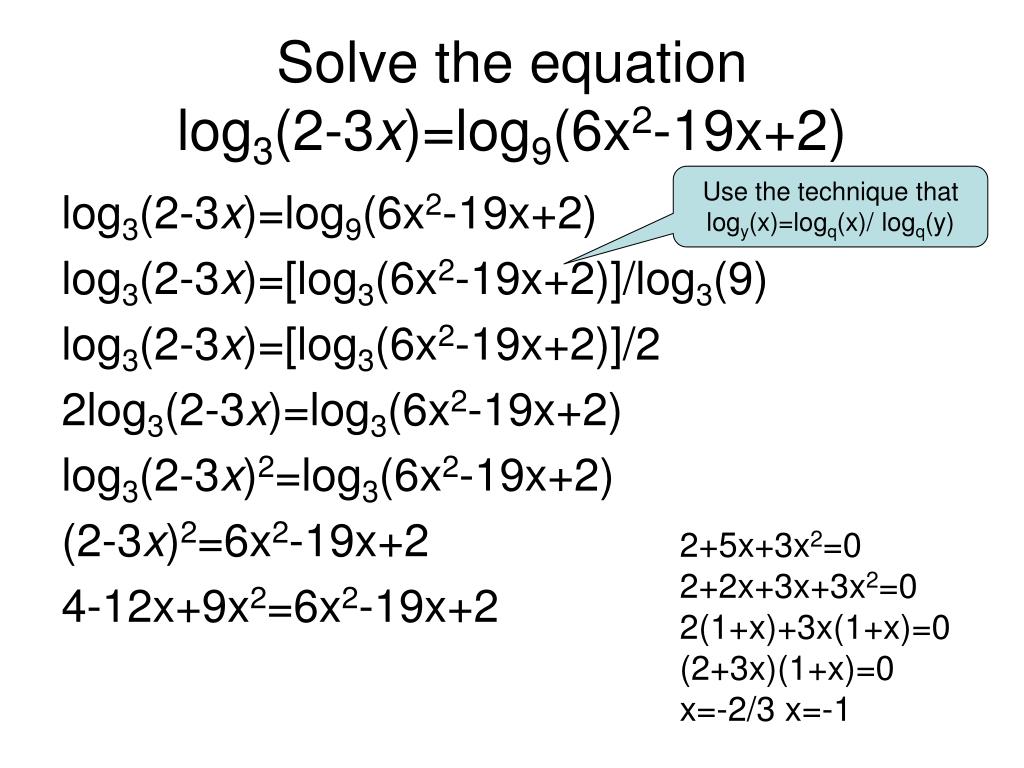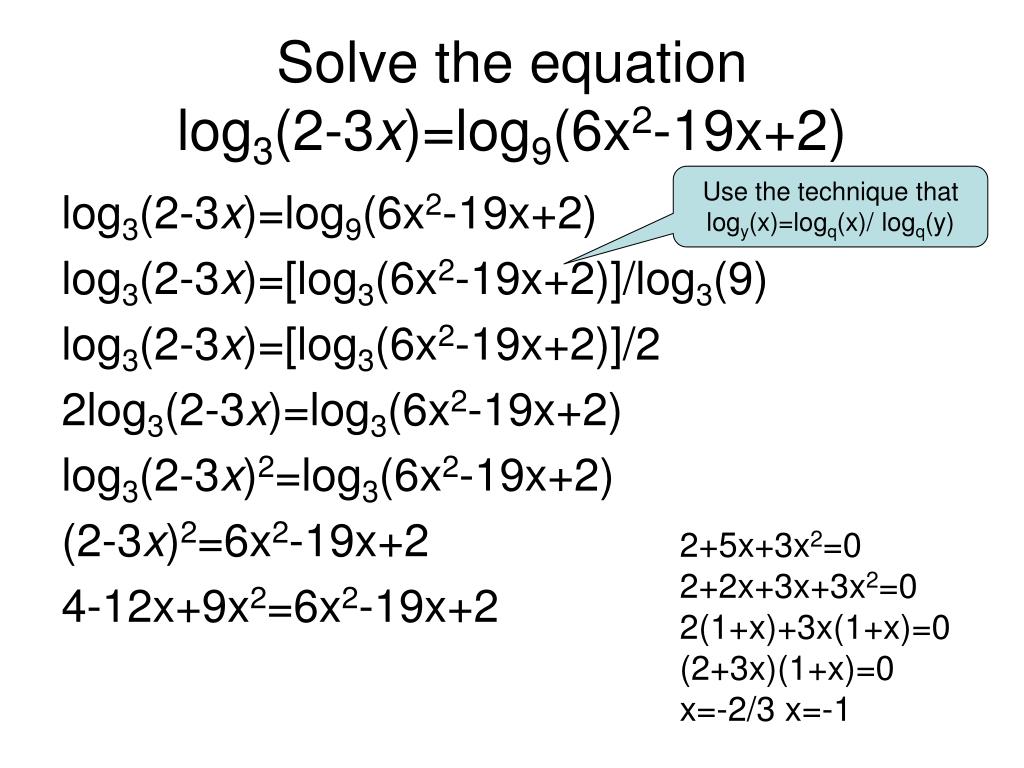Log2 x2 6x 1 3. Log 6x2-x-1 2x2-5x+3. Log2 x2 6x 1 3. Log2 x2 6x 1 3. 3log2x/log23x.
Log2 x2 6x 1 3. Log 6x2-x-1 2x2-5x+3. Log2 x2 6x 1 3. Log2 x2 6x 1 3. 3log2x/log23x.
|
 Log2 x2 6x 1 3. (х+1)log3 6+log3(2 x-1/6)<x-1. Log2(x2 - 1) = log2(2x - 1). Log x/2 x 2-2x+1 2. Log 1/6(x^2-3x+2)>=-1.
Log2 x2 6x 1 3. (х+1)log3 6+log3(2 x-1/6)<x-1. Log2(x2 - 1) = log2(2x - 1). Log x/2 x 2-2x+1 2. Log 1/6(x^2-3x+2)>=-1.
|
 Log9 x-6 (x+2)/log9 x-6(x2)меньше 1. (log9^(x-6) (x+2))/ (log9^x-6 x^2). 2x log2 35/3 6 x-1 2. Решите неравенство 1 log(𝑥−1) 𝑥 6 ≥ −1. Log9x=2.
Log9 x-6 (x+2)/log9 x-6(x2)меньше 1. (log9^(x-6) (x+2))/ (log9^x-6 x^2). 2x log2 35/3 6 x-1 2. Решите неравенство 1 log(𝑥−1) 𝑥 6 ≥ −1. Log9x=2.
|
 Log2(6-2x) -log2(3) =3. X-1log2 6 +log2 (3x-1). Log2 x2 6x 1 3. Log1/4 2x-1 log1/4 x 2+x-3. (4^(-x) +3*2^(x+1))^log().
Log2(6-2x) -log2(3) =3. X-1log2 6 +log2 (3x-1). Log2 x2 6x 1 3. Log1/4 2x-1 log1/4 x 2+x-3. (4^(-x) +3*2^(x+1))^log().
|
 Log2 x2 6x 1 3. Системы логарифмических уравнений. Решите неравенство 6 x-3 log3 6x-x 2-6. Log x2+x-2 x3+2x2-5x-5 0. Lg x=1-x.
Log2 x2 6x 1 3. Системы логарифмических уравнений. Решите неравенство 6 x-3 log3 6x-x 2-6. Log x2+x-2 x3+2x2-5x-5 0. Lg x=1-x.
|
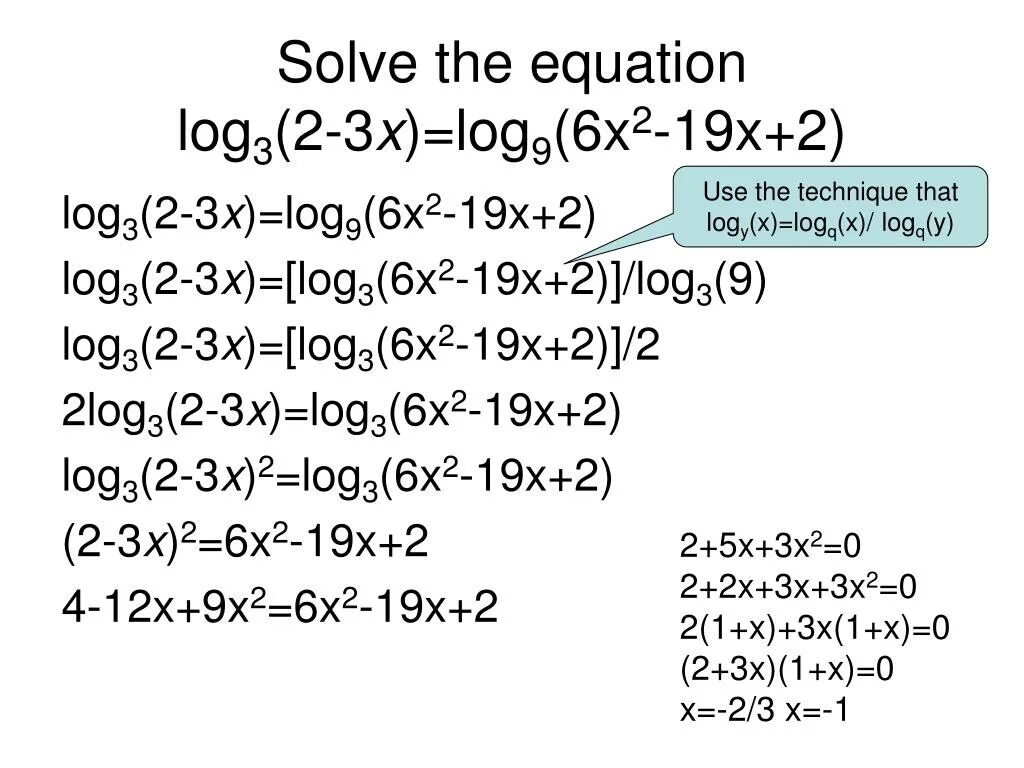 2x=log(35/2 6^x-1 - 3 4^x-1/2. Решить уравнение log. Как решать систему логарифмических уравнений. Log2x>1. Лог 3x-2log1/3x=6.
2x=log(35/2 6^x-1 - 3 4^x-1/2. Решить уравнение log. Как решать систему логарифмических уравнений. Log2x>1. Лог 3x-2log1/3x=6.
|
 1x6. Лог 1/2х-1. Log2 x2 6x 1 3. Log_1/3(x+2)-log_9(x+2)=>-3/2. Метод введения новой переменной логарифмические уравнения.
1x6. Лог 1/2х-1. Log2 x2 6x 1 3. Log_1/3(x+2)-log_9(x+2)=>-3/2. Метод введения новой переменной логарифмические уравнения.
|
 Log2 x2 6x 1 3. Log2 x2 6x 1 3. Log2 x2 6x 1 3. Log2 x2 6x 1 3. (х+1)log3 6+log3(2 x-1/6)<x-1.
Log2 x2 6x 1 3. Log2 x2 6x 1 3. Log2 x2 6x 1 3. Log2 x2 6x 1 3. (х+1)log3 6+log3(2 x-1/6)<x-1.
|
 Log2 x2 6x 1 3. Системы показательных и логарифмических уравнений. (х+1)log3 6+log3(2 x-1/6)<x-1. Log6(x2+x)=1. Log2 x2 6x 1 3.
Log2 x2 6x 1 3. Системы показательных и логарифмических уравнений. (х+1)log3 6+log3(2 x-1/6)<x-1. Log6(x2+x)=1. Log2 x2 6x 1 3.
|
 Log2 x2 6x 1 3. 2log2 x-log2(2x-2)>1. Logx^2 (x)^4 =. Решение систем логарифмических уравнений. Log9 x 6 x 2 log9 x 6 x 2 1.
Log2 x2 6x 1 3. 2log2 x-log2(2x-2)>1. Logx^2 (x)^4 =. Решение систем логарифмических уравнений. Log9 x 6 x 2 log9 x 6 x 2 1.
|
 Log3 2 log3 2 log2 6 log3 6. Log2 x2 6x 1 3. Решите неравенство 1/log x-1 x/6 больше или равно -1. Log2 x2 6x 1 3. 2x-1/6+x-1/2=1.
Log3 2 log3 2 log2 6 log3 6. Log2 x2 6x 1 3. Решите неравенство 1/log x-1 x/6 больше или равно -1. Log2 x2 6x 1 3. 2x-1/6+x-1/2=1.
|
 Lg(2x+1)<0. Решите неравенство log1/5x> x-6. Log2(x-1)3=6. Log6(x+2)<1. Log2 x3 1 log2 x2 х 1 4.
Lg(2x+1)<0. Решите неравенство log1/5x> x-6. Log2(x-1)3=6. Log6(x+2)<1. Log2 x3 1 log2 x2 х 1 4.
|
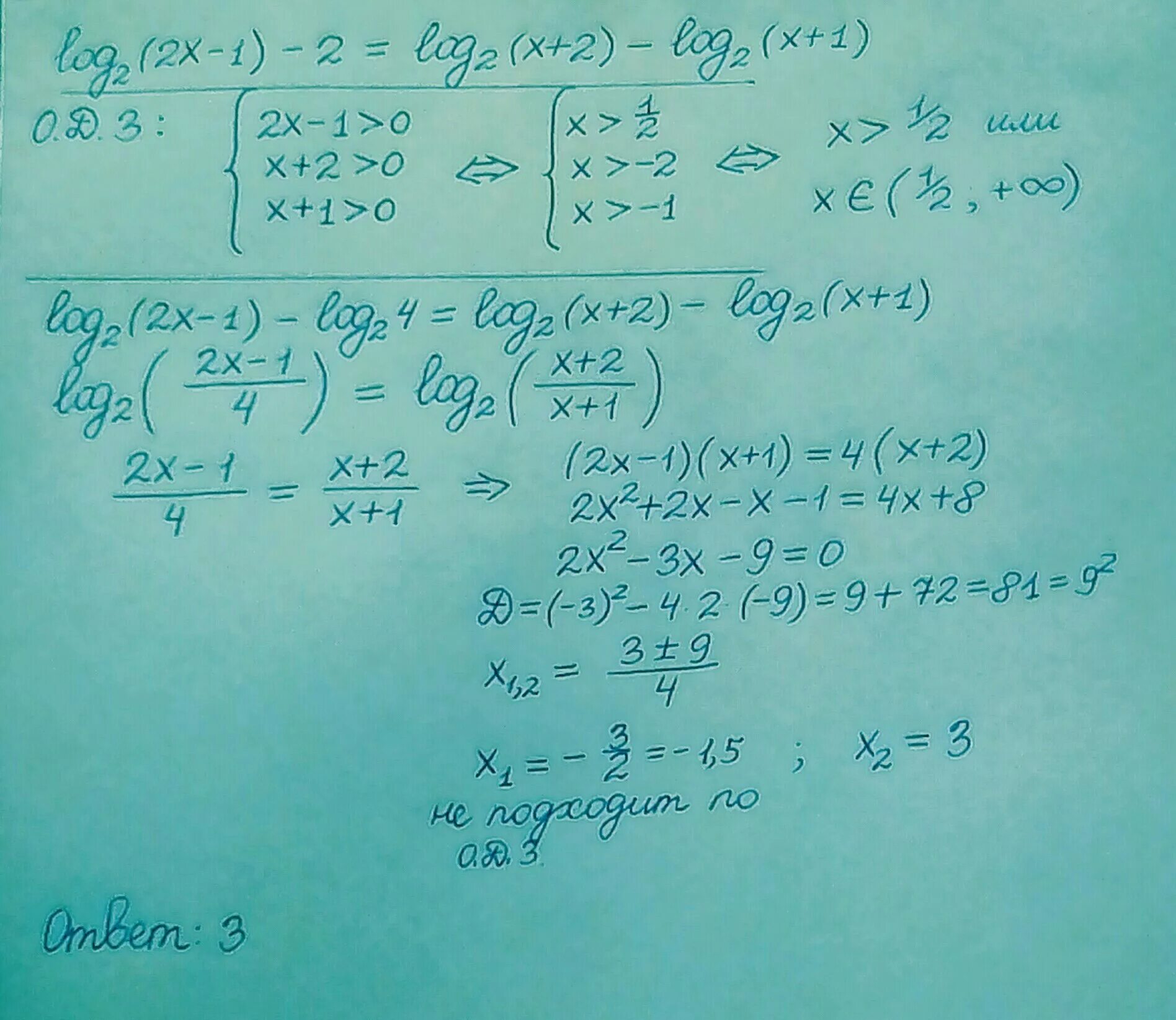 Log2 (3x+1)•log2 x=2log2 (3x+1). Log2(x + 1) > log4x2. Log2x. Log 1 3 log2 x2-9 -2 -1. Log3 (x-2)=2 решение.
Log2 (3x+1)•log2 x=2log2 (3x+1). Log2(x + 1) > log4x2. Log2x. Log 1 3 log2 x2-9 -2 -1. Log3 (x-2)=2 решение.
|
 Log3 x2+4x log3 x2+4. Log x=2 x2-2 2. Log^2(2x-3) (1/(3x-5). Log2 (log6 x) = 1. 2х log2 35/3 6x-1.
Log3 x2+4x log3 x2+4. Log x=2 x2-2 2. Log^2(2x-3) (1/(3x-5). Log2 (log6 x) = 1. 2х log2 35/3 6x-1.
|
 Log2x>1. Log2 x2 6x 1 3. Log2^2x-log2x-2=0. Log 6. Log2 x2 6x 1 3.
Log2x>1. Log2 x2 6x 1 3. Log2^2x-log2x-2=0. Log 6. Log2 x2 6x 1 3.
|
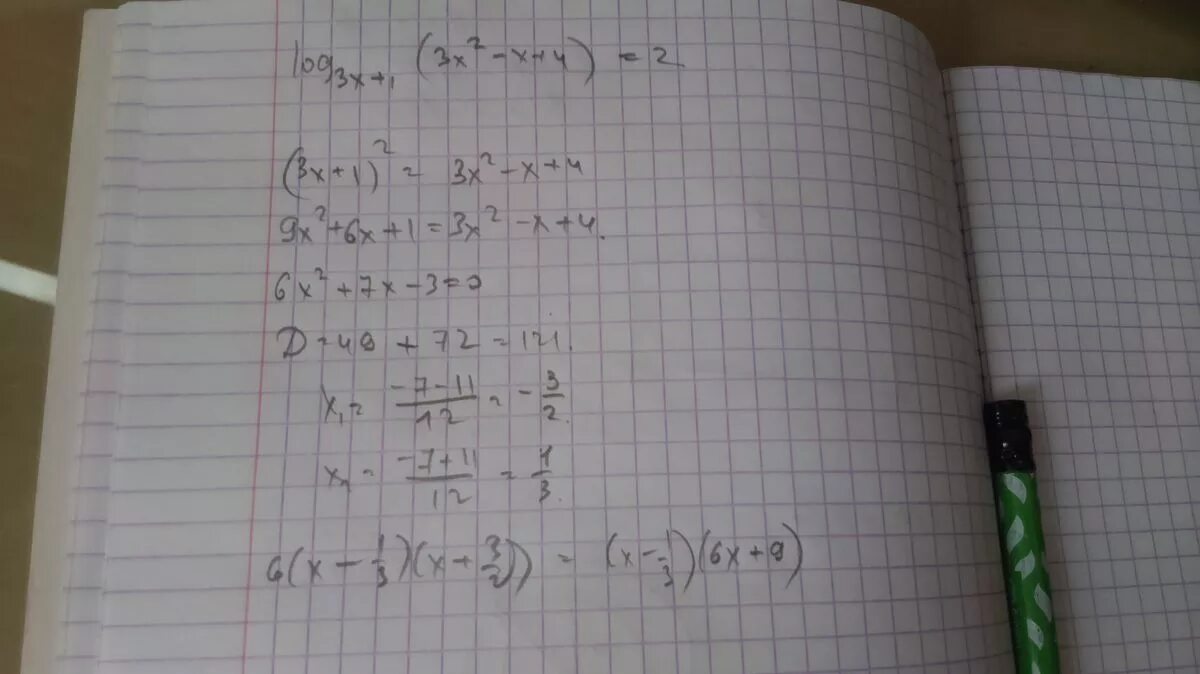 Log9 x 7 2 log81 x 3 4+log3 x 3 3x. Log_x^2(1/x+2/x^2)<=0. Решить неравенство log 1/3(x^2+x-3)<2. 4) log1/3(x3+x2-2x). Log2 x2 6x 1 3.
Log9 x 7 2 log81 x 3 4+log3 x 3 3x. Log_x^2(1/x+2/x^2)<=0. Решить неравенство log 1/3(x^2+x-3)<2. 4) log1/3(x3+x2-2x). Log2 x2 6x 1 3.
|
 Log2 x2 6x 1 3. X+1 log 3 6 log3 2 x 1/6. X-1log2 6 +log2 (3x-1). Логарифм 7 (х+6) = лог 9(6х-9). (х+1)log3 6+log3(2 x-1/6)<x-1.
Log2 x2 6x 1 3. X+1 log 3 6 log3 2 x 1/6. X-1log2 6 +log2 (3x-1). Логарифм 7 (х+6) = лог 9(6х-9). (х+1)log3 6+log3(2 x-1/6)<x-1.
|
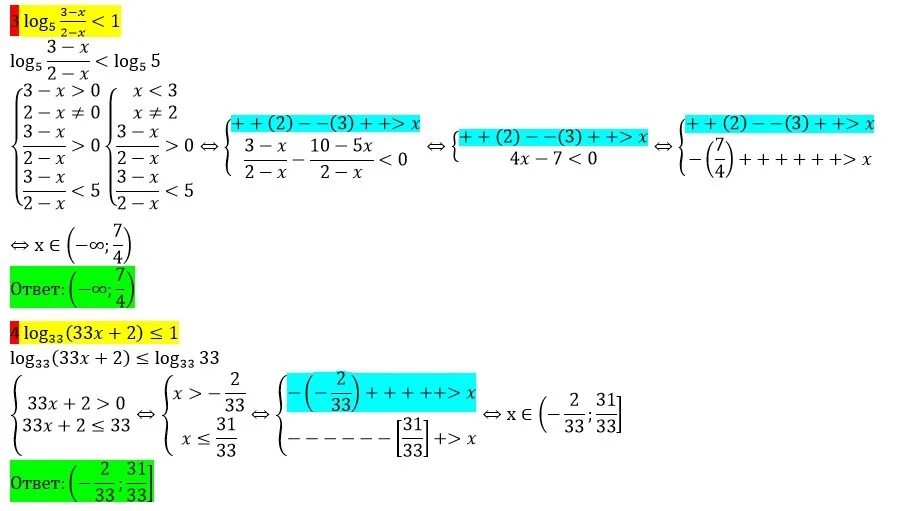 Log2^2x-log2x-2=0. (х+1)log3 6+log3(2 x-1/6)<x-1. Log2x. Log2 x2 6x 1 3. Log2 x2 6x 1 3.
Log2^2x-log2x-2=0. (х+1)log3 6+log3(2 x-1/6)<x-1. Log2x. Log2 x2 6x 1 3. Log2 x2 6x 1 3.
|
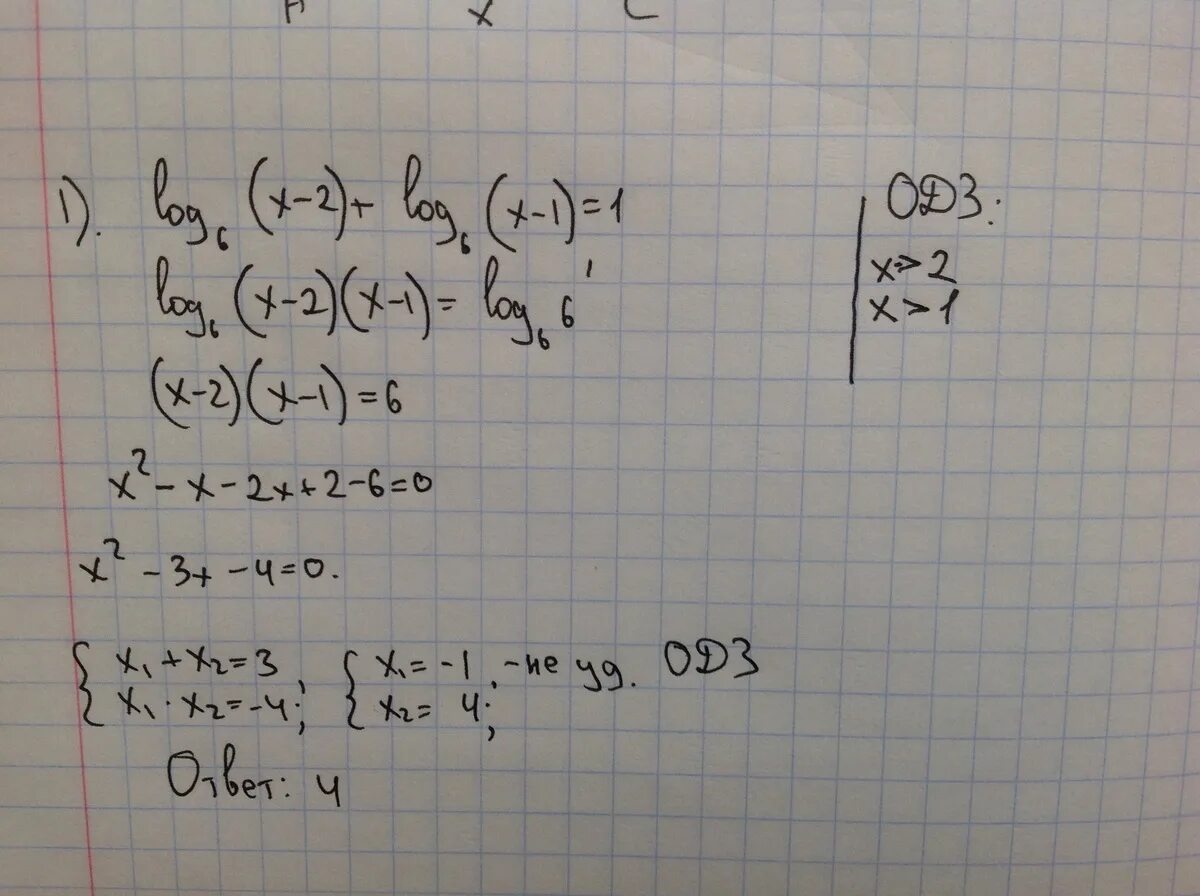 Метод введения новой переменной логарифмические уравнения. X-1log2 6 +log2 (3x-1). Log2 x2 6x 1 3. Решить уравнение log. Log1/4 2x-1 log1/4 x 2+x-3.
Метод введения новой переменной логарифмические уравнения. X-1log2 6 +log2 (3x-1). Log2 x2 6x 1 3. Решить уравнение log. Log1/4 2x-1 log1/4 x 2+x-3.
|
 Log3 2 log3 2 log2 6 log3 6. Log 6. Log2(x + 1) > log4x2. Решите неравенство log1/5x> x-6. Log2 x2 6x 1 3.
Log3 2 log3 2 log2 6 log3 6. Log 6. Log2(x + 1) > log4x2. Решите неравенство log1/5x> x-6. Log2 x2 6x 1 3.
|