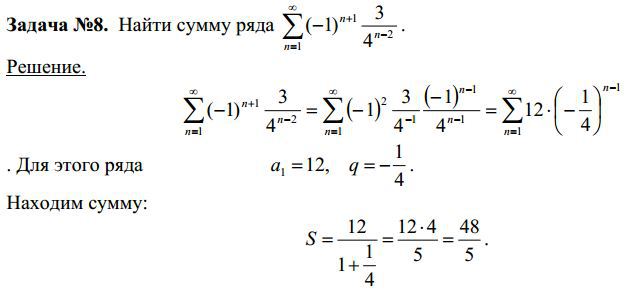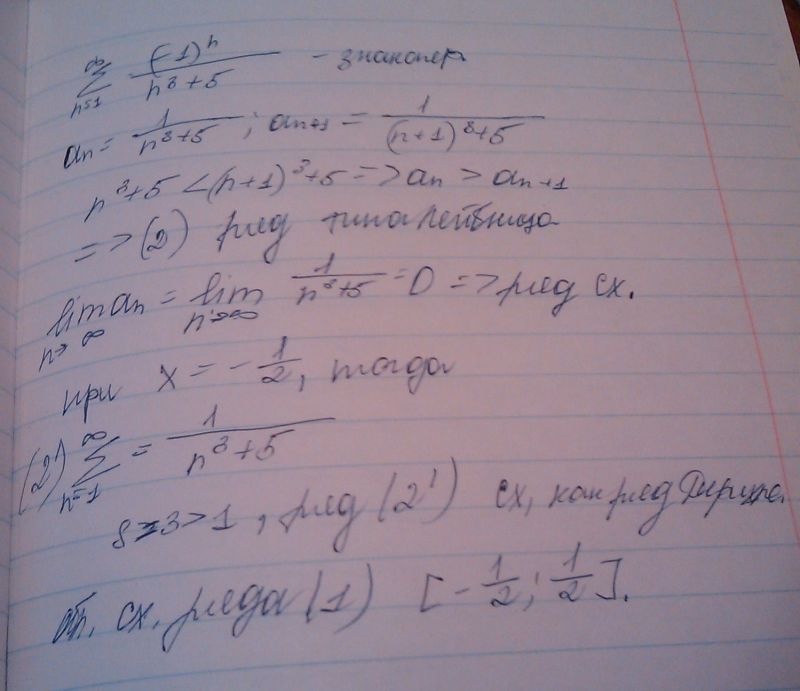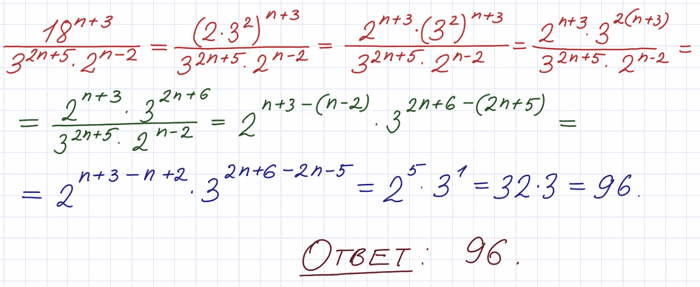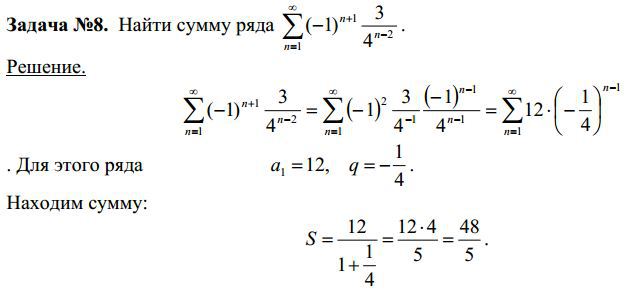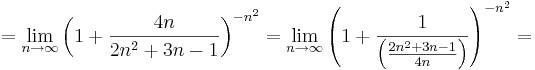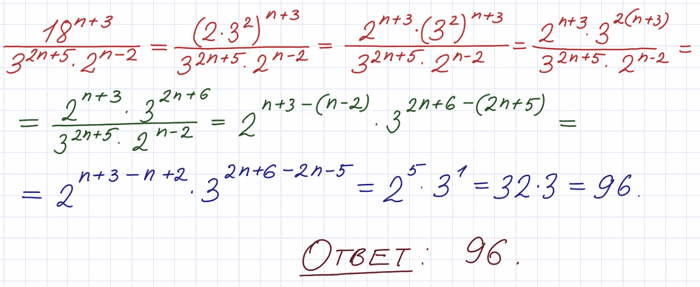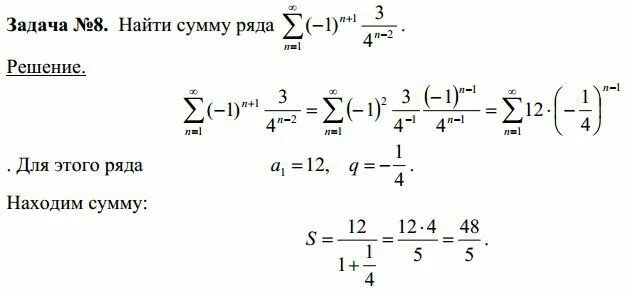 ряд (-1)^n/n. $2^{2^n-2^n}=2^{2^n-n}$. исследовать ряд на сходимость. решение пределов с бесконечностью. N 3 x n 5. ряд (-1)^n/n. $2^{2^n-2^n}=2^{2^n-n}$. исследовать ряд на сходимость. решение пределов с бесконечностью. N 3 x n 5. |  ряд 1/n+1. приведите подобные слагаемые -4n +n +2n. Xn=2n+5. 2n+2-2n-2/2n сократить. что такое n частичная сумма ряда. ряд 1/n+1. приведите подобные слагаемые -4n +n +2n. Xn=2n+5. 2n+2-2n-2/2n сократить. что такое n частичная сумма ряда. |
 N 3 x n 5. ряд (-1)^n/(n^1/2+ln(n)). N 3 x n 5. (5 n-2)^2-(2n-5)^2. N(n-1)/2. N 3 x n 5. ряд (-1)^n/(n^1/2+ln(n)). N 3 x n 5. (5 n-2)^2-(2n-5)^2. N(n-1)/2. |  (n+4)(2+n). 3n/2. сходимость ряда x^n/(n+1)!. N 3 x n 5. решение ряда 2n+1/n(n+2). (n+4)(2+n). 3n/2. сходимость ряда x^n/(n+1)!. N 3 x n 5. решение ряда 2n+1/n(n+2). |
 Lim n!(n+2)/(n+2)!-n!. ряды найти сумму ряда. дробь 45𝑛32𝑛−1⋅5𝑛−2 45 n 3 2 n − 1 ⋅ 5 n − 2. ((n+1)/n)^2n^2. сходимость ряда ((x+1)^n)/n*4^n-1. Lim n!(n+2)/(n+2)!-n!. ряды найти сумму ряда. дробь 45𝑛32𝑛−1⋅5𝑛−2 45 n 3 2 n − 1 ⋅ 5 n − 2. ((n+1)/n)^2n^2. сходимость ряда ((x+1)^n)/n*4^n-1. |  ряд 1/n^2. исследовать сходимость числового ряда. Lim n+1/n+2. (2n-1)/2^n. N(n-1)/2. ряд 1/n^2. исследовать сходимость числового ряда. Lim n+1/n+2. (2n-1)/2^n. N(n-1)/2. |
 Lim (2n)!/a^(n!). привести подобные 3x+5y. (2n+1)(2n-1). сходимость ряда 1/ln n. N 3 x n 5. Lim (2n)!/a^(n!). привести подобные 3x+5y. (2n+1)(2n-1). сходимость ряда 1/ln n. N 3 x n 5. |  Lim 1 n2 2 n2 n 1 n2. N 3 x n 5. 2^n+1 + 2^n-2. исследование на сходимость степенной ряд. Lim 3*n^2/((2 - n)^2) - 1*3 14 вариант. Lim 1 n2 2 n2 n 1 n2. N 3 x n 5. 2^n+1 + 2^n-2. исследование на сходимость степенной ряд. Lim 3*n^2/((2 - n)^2) - 1*3 14 вариант. |
 N 3 x n 5. 5 n+1 5 n-1 2 5n n 1. N=2n2. 50n/5n-1 2n-1. сумма ряда 1/n 2. N 3 x n 5. 5 n+1 5 n-1 2 5n n 1. N=2n2. 50n/5n-1 2n-1. сумма ряда 1/n 2. |  N 3 x n 5. Lim (2n)!/a^(n!). N-3-n0-n+2-n+1-n+3. ряд (2n-1)!!/n!. N 3 x n 5. N 3 x n 5. Lim (2n)!/a^(n!). N-3-n0-n+2-n+1-n+3. ряд (2n-1)!!/n!. N 3 x n 5. |
 N 3 x n 5. (2n-1)!<n^(2n-1). числовой ряд n-1 n3+2. (2n+1)(2n-1). сократите дробь 18 n+3/3 2n+5. N 3 x n 5. (2n-1)!<n^(2n-1). числовой ряд n-1 n3+2. (2n+1)(2n-1). сократите дробь 18 n+3/3 2n+5. |  $2^{2^n-2^n}=2^{2^n-n}$. сследовть нас ходимость ряд. N 3 x n 5. 3n2 n 1/5n2 14n 5 пределы. исследование числовых рядов на сходимость. $2^{2^n-2^n}=2^{2^n-n}$. сследовть нас ходимость ряд. N 3 x n 5. 3n2 n 1/5n2 14n 5 пределы. исследование числовых рядов на сходимость. |
 1 2 2 2 n n n. предел при x стремящемся к бесконечности. (n^2+6n+5)x^(n+1) сумма ряда. A n+1 = 2a n - 3. ряд (-1)^n/n. 1 2 2 2 n n n. предел при x стремящемся к бесконечности. (n^2+6n+5)x^(n+1) сумма ряда. A n+1 = 2a n - 3. ряд (-1)^n/n. |  N 3 x n 5. N 3 x n 5. (2n-1)/2^n. N 3 x n 5. (-1) ^n*4n^3/(n^4+4). N 3 x n 5. N 3 x n 5. (2n-1)/2^n. N 3 x n 5. (-1) ^n*4n^3/(n^4+4). |
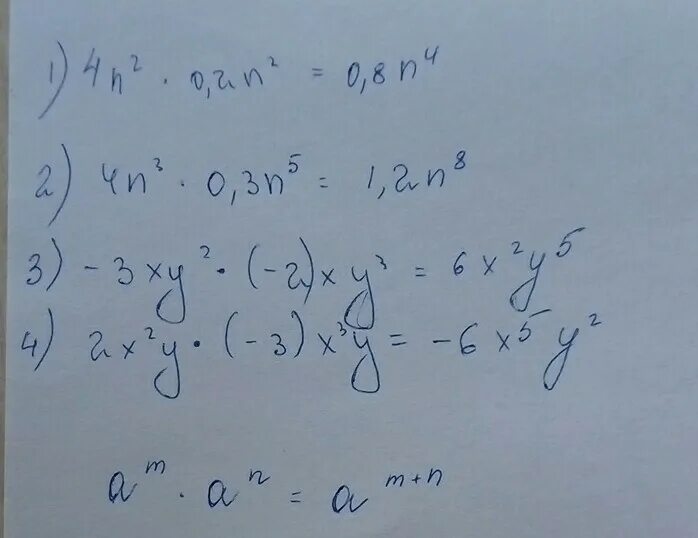 N 3 x n 5. ∑_(n=1)^∞(n/(2n+1) )^(n ) 〗. примеры на вычисление. 1-1/n+2. сократите дробь 18 n+3/3 2n+5 2 n-2. N 3 x n 5. ∑_(n=1)^∞(n/(2n+1) )^(n ) 〗. примеры на вычисление. 1-1/n+2. сократите дробь 18 n+3/3 2n+5 2 n-2. |  сократите дробь 18n+3 /3 2n+5 2n-2. N2n. N 3 x n 5. N 3 x n 5. (2n-1)/2^n. сократите дробь 18n+3 /3 2n+5 2n-2. N2n. N 3 x n 5. N 3 x n 5. (2n-1)/2^n. |
 сходимость ряда 2n+1/(n(n+1)). N 3 x n 5. сходимость ряда ln n /n 2. N+5 n+4. Lim=(√(3n+1)-√(n+2)). сходимость ряда 2n+1/(n(n+1)). N 3 x n 5. сходимость ряда ln n /n 2. N+5 n+4. Lim=(√(3n+1)-√(n+2)). | 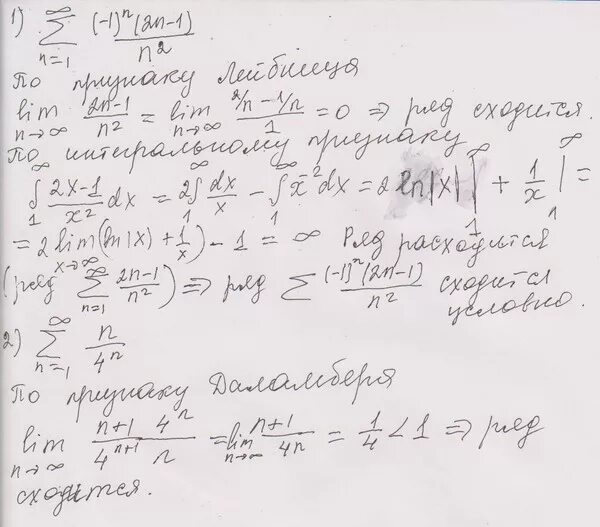 дробь:n!(n+1)!. N 3 x n 5. N 3 x n 5. Lim n+1/n+2. ряд (-1)^n*(2n)!!/(2n+1)!! сходимость. дробь:n!(n+1)!. N 3 x n 5. N 3 x n 5. Lim n+1/n+2. ряд (-1)^n*(2n)!!/(2n+1)!! сходимость. |
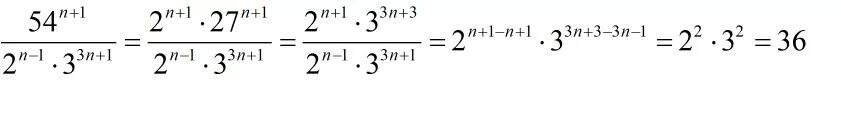 ряд n+2/2n+1 ^3n+1. исследовать на сходимость ряд (-1)^n * (n/n^3+1)). как найти сумму ряда. предел n стремится к бесконечности. факториал (n+2)!/n!. ряд n+2/2n+1 ^3n+1. исследовать на сходимость ряд (-1)^n * (n/n^3+1)). как найти сумму ряда. предел n стремится к бесконечности. факториал (n+2)!/n!. |  сократить 18^n+3/3 2n+5 2 n-2. 4+4n+n2. ряд 1/2n-1. 5n - n. Lim (2n)!/a^(n!). сократить 18^n+3/3 2n+5 2 n-2. 4+4n+n2. ряд 1/2n-1. 5n - n. Lim (2n)!/a^(n!). |